DFS深度优先
岛屿最大面积

深度优先算法的重要思想就是借助栈每次访问栈顶的元素
而递归就无需我们手动压入栈当中了,我们需要做的是判断栈顶元素是否已经访问,并且每次递归调用(压入栈)的应该是栈顶元素的邻接节点。
这道题非常的特殊,0表示没有岛屿,1表示是岛屿,那么每次压入栈的邻接节点应该值应是1的,并且可以通过将已经访问的元素置为0,表示栈顶元素已经访问以避免重复访问。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
int des[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
int m,n;
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int maxs = 0;
m = grid.size();
n = grid[0].size();
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
int s = 0;
if(grid[i][j] == 1){
dfs(i,j,grid,s);
maxs = max(maxs,s);
}
}
}
return maxs;
}
void dfs(int i,int j,vector<vector<int>>& grid,int &s){
grid[i][j] = 0;
s++;
for (int k = 0; k < 4; k++) {
int tmpi = i + des[k][0];
int tmpj = j + des[k][1];
if (tmpi < 0 || tmpi >= m || tmpj < 0 || tmpj >= n || grid[tmpi][tmpj] == 0)continue;
dfs(tmpi, tmpj, grid,s);
}
}
};
|
省份数量
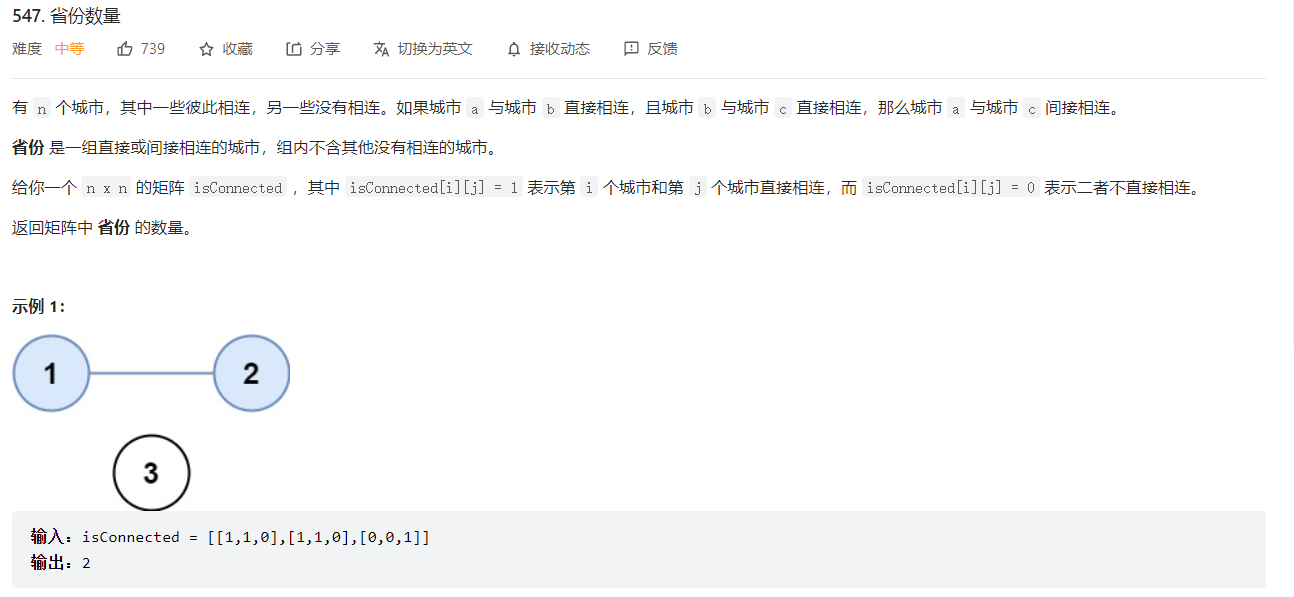
记住dfs的本质:借助栈来遍历,每次访问栈顶的元素,并且将栈顶元素的邻接节点加入栈中,注意每次访问的时候要判断栈顶元素是否已经访问过了。
而我们借助递归,无需我们手动构建栈了,但是一定要注意,递归参数就是邻接节点,
dfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
int m, n;
vector<bool>visited;
public:
int findCircleNum(vector<vector<int>>& isConnected) {
m = isConnected.size();
n = isConnected[0].size();
visited = vector<bool>(m,false);
int sum = 0;
for(int i = 0;i < m;i++){
if(!visited[i]){
sum++;
dfs(isConnected,i);
}
}
return sum;
}
void dfs(vector<vector<int>>& isConnected,int cur){
visited[cur] = true;
for(int i = 0;i < n;i++){
if(visited[i] == true || isConnected[cur][i] == 0)continue;
dfs(isConnected,i);
}
}
};
|
回溯感觉讲究的是所有可能的方向都枚举出来,然后对部分枚举结果进行剪枝操作(即做一定的选择)。而且后面一定要撤销之前的选择。
1
2
3
4
5
6
7
8
9
10
| result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
|
这一题关键在于for循环对所有的数组所有的值进行递归操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
vector<vector<int>>ans;
vector<vector<int>> permute(vector<int>& nums) {
vector<int>res;
vector<bool> visited(nums.size(),false);
dfs(nums,0,res,visited);
return ans;
}
void dfs(vector<int>& nums,int s,vector<int>&res,vector<bool>&visited){
if(s == nums.size()){
ans.push_back(res);
return;
}
for(int i = 0;i < nums.size();i++){
if(!visited[i]){
visited[i] = true;
res.push_back(nums[i]);
dfs(nums,s+1,res,visited);
res.pop_back();
visited[i] = false;
}
}
}
};
|
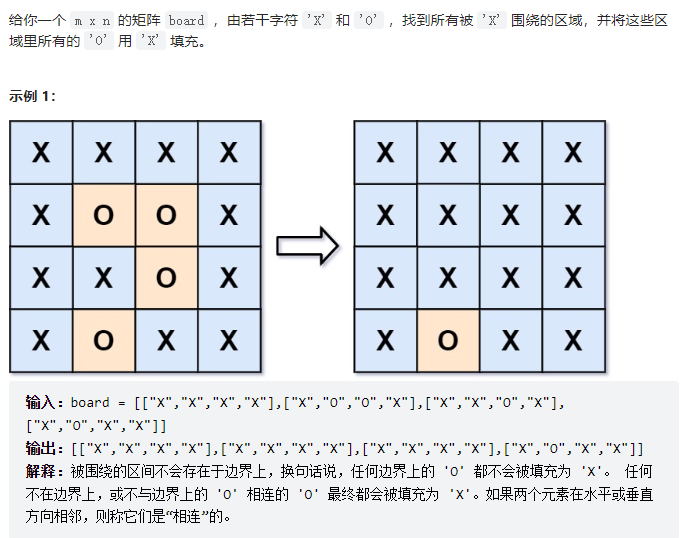
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
vector<vector<bool>>visited;
int m, n;
int des[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
public:
void solve(vector<vector<char>>& board) {
m = board.size();
n = board[0].size();
visited = vector<vector<bool>>(m,vector<bool>(n,false));
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if((i == 0 || i == m-1 || j==0 || j == n-1 )&& (board[i][j] == 'O'))
dfs(board,i,j);
}
}
for(int i = 1;i < m - 1;i++){
for(int j = 1;j < n - 1;j++){
if(board[i][j] == 'O' && visited[i][j] == false)board[i][j] = 'X';
}
}
return;
}
void dfs(vector<vector<char>>& graph, int i, int j) {
if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || graph[i][j] == 'X')return;
visited[i][j] = true;
for (int k = 0; k < 4; k++) {
int tmpi = i + des[k][0];
int tmpj = j + des[k][1];
dfs(graph, tmpi, tmpj);
}
}
};
|
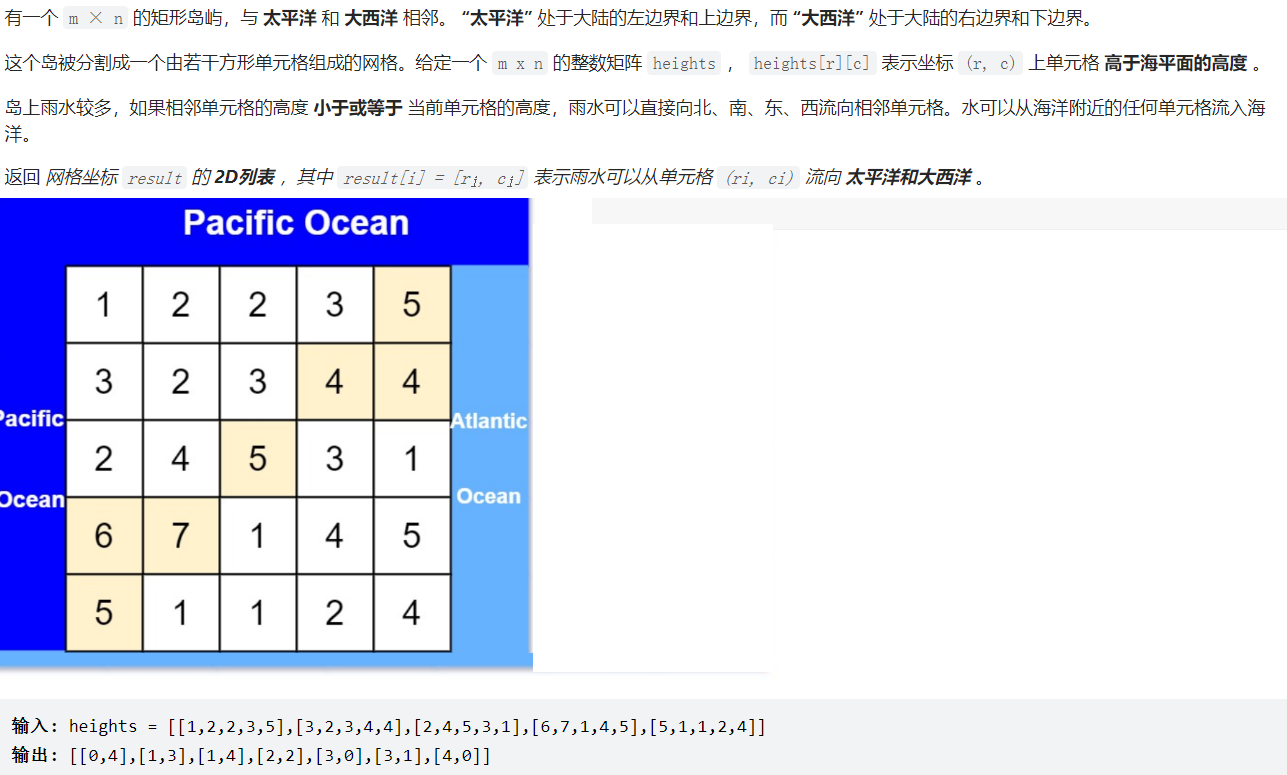
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public:
vector<vector<bool>>visited1;
vector<vector<bool>>visited2;
int des[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
int m,n;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m = heights.size();n = heights[0].size();
visited1 = vector<vector<bool>>(m,vector<bool>(n,false));
visited2 = vector<vector<bool>>(m,vector<bool>(n,false));
for(int i = 0;i < m;i++)dfs(heights,visited1,i,0);
for(int i = 0;i < n;i++)dfs(heights,visited1,0,i);
for(int i = 0;i < m;i++)dfs(heights,visited2,i,n-1);
for(int i = 0;i < n;i++)dfs(heights,visited2,m-1,i);
vector<vector<int>>results;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(visited1[i][j] && visited2[i][j]){
results.push_back(vector<int>{i,j});
}
}
}
return results;
}
void dfs(vector<vector<int>>& heights,vector<vector<bool>>&visited,int i,int j){
visited[i][j] = true;
for(int k = 0;k < 4;k++){
int tmpi = i + des[k][0];
int tmpj = j + des[k][1];
if(tmpi < 0 || tmpj < 0 || tmpi >= m || tmpj >= n
|| visited[tmpi][tmpj] || heights[tmpi][tmpj] < heights[i][j])continue;
dfs(heights,visited,tmpi,tmpj);
}
}
};
|
回溯与DFS区别:
例如对于一个遍历矩阵
第一次遍历如下

如果是回溯,那么下一次遍历还可能访问C和D

如果是图visited[i] = true放在for前面,如果是数组选择的那么visited[i] = true放在for后面
回溯
回溯法解决的问题都可以抽象为树形结构,因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
递归树上的每一个节点包括1.子集(当前遍历路径上的所有元素构成子集)和2.剩余集合(剩下可以选择的元素构成集合)
1
2
3
4
5
6
7
8
9
10
11
12
| void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;不符合条件的continue
backtracking(路径,选择列表);
回溯,撤销处理结果
}
}
|
1.递归树
2.终止条件:
3.选择列表
4.判断是否需要剪枝
5.做出选择
6.撤销选择
全排列
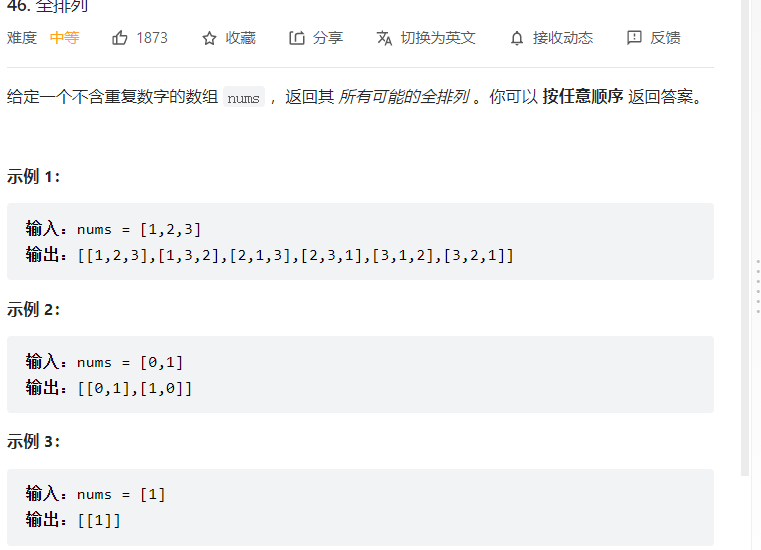
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
vector<vector<int>>ans;
vector<int>res;
vector<bool>visited;
vector<vector<int>> permute(vector<int>& nums) {
vector<bool>v(nums.size(),false);
visited = v;
dfs(nums,0);
return ans;
}
void dfs(vector<int>& nums,int s){
if(s == nums.size()){
ans.push_back(res);
return;
}
for(int i = 0;i < nums.size();i++){
if(visited[i])continue;
else{
visited[i] = true;
res.push_back(nums[i]);
dfs(nums,s+1);
res.pop_back();
visited[i] = false;
}
}
}
};
|
全排列2
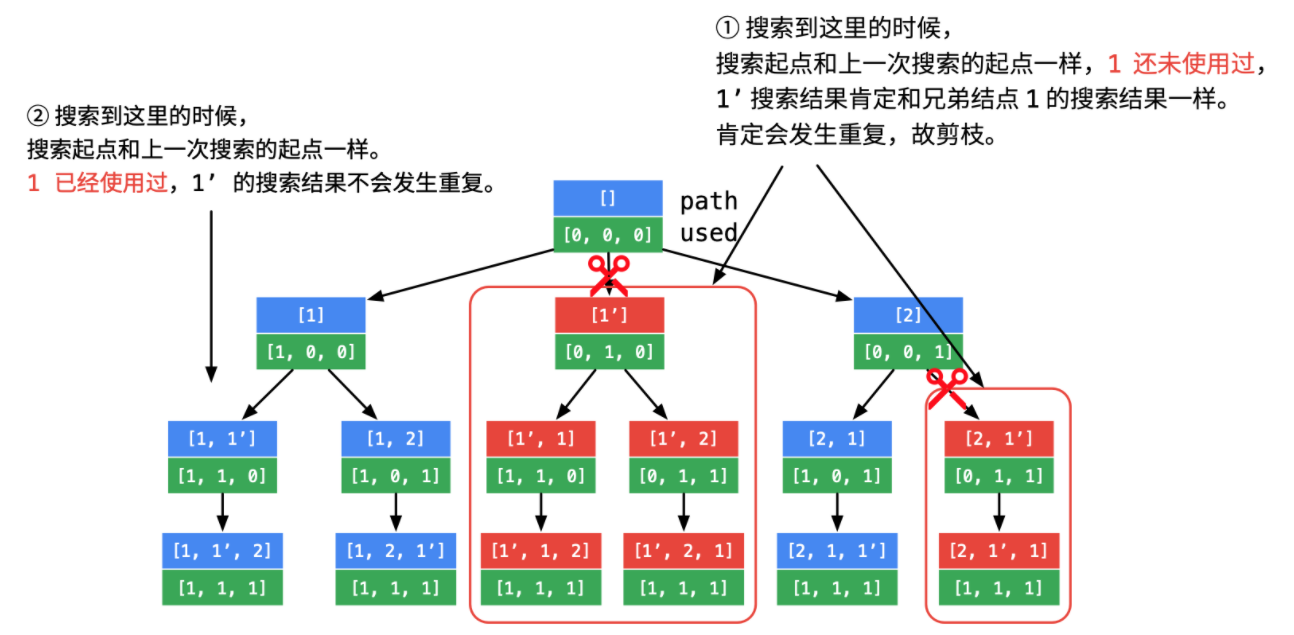
我们需要将其重新排序,并且仅仅需要在多加一个判断
else if(i > 0 && nums[i]==nums[i-1] && !visited[i-1])continue;//前面重复的1被选择了但被撤销了应该删除
为什么是这样一个判断,因为这个判断是用于删除同一层的分支的,避免删除同一列的分支情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
vector<vector<int>>ans;
vector<int>res;
vector<bool>visited;
vector<vector<int>> permuteUnique(vector<int>& nums) {
visited = vector<bool>(nums.size(),false);
sort(nums.begin(),nums.end());
dfs(nums,0);
return ans;
}
void dfs(vector<int>& nums,int s){
if(s == nums.size()){
ans.push_back(res);
return;
}
for(int i = 0;i < nums.size();i++){
if(visited[i])continue;
else if(i > 0 && nums[i]==nums[i-1] && !visited[i-1])continue;
else{
visited[i] = true;
res.push_back(nums[i]);
dfs(nums,s+1);
res.pop_back();
visited[i] = false;
}
}
}
};
|
谨记回溯模板
1
2
3
4
5
6
7
8
9
10
11
12
| void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;不符合条件的continue
backtracking(路径,选择列表);
回溯,撤销处理结果
}
}
|
子集问题稍有变换,本质还是这个模板,终止条件存放结果,未终止的话就处理节点递归
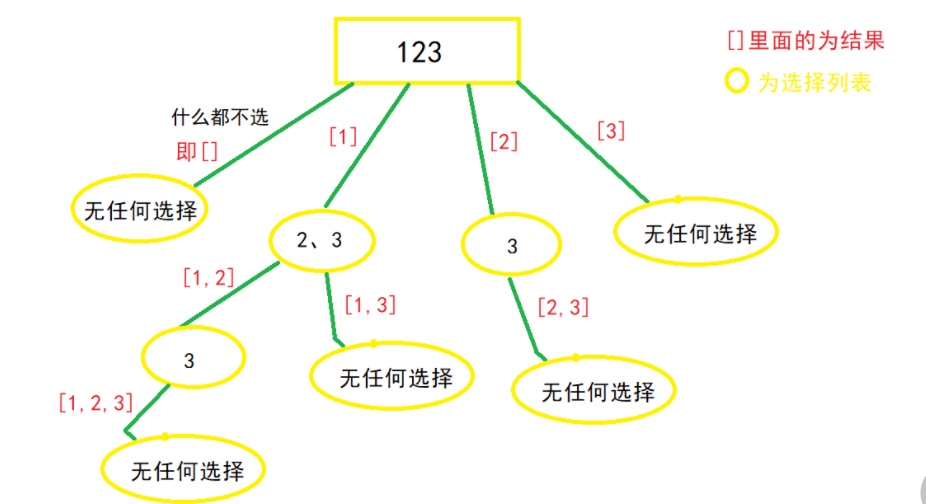
子集对于每一个中间过程都应该存入,因此没有终止条件,每一个过程节点都应存放结果
对于本层集合中元素,是上一个元素的后一位置开始选择而不是从0开始
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
vector<vector<int>>res;
vector<int>r;
vector<vector<int>> subsets(vector<int>& nums) {
dfs(nums,0);
return res;
}
void dfs(vector<int>&nums,int start){
res.push_back(r);
for(int j = start;j < nums.size();j++){
r.push_back(nums[j]);
dfs(nums,j+1);
r.pop_back();
}
}
};
|
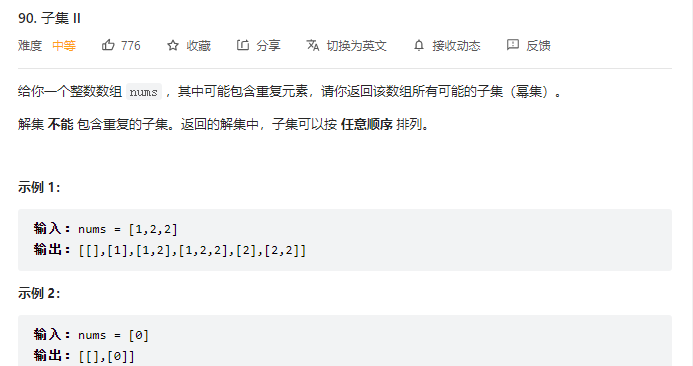
类似的像全排列2那样新加判断即可
if(i > start&&nums[i] == nums[i-1])continue;这个判断是用于删除同一层的分支的,避免删除同一列的分支情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
vector<vector<int>>res;
vector<int>r;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(),nums.end());
dfs(nums,0);
return res;
}
void dfs(vector<int>&nums,int start){
res.push_back(r);
for(int i = start;i < nums.size();i++){
if(i > start&&nums[i] == nums[i-1])continue;
r.push_back(nums[i]);
dfs(nums, i + 1);
r.pop_back();
}
}
};
|
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
1
2
3
4
5
6
7
8
9
10
| 输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
|
示例 2:
1
2
| 输入:n = 1, k = 1
输出:[[1]]
|
提示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
void printvector(vector<int>path,string l,string r){
cout << l;
for(auto v : path){
cout << v << ", ";
}
cout <<r<<endl;
}
vector<vector<int>>results;
vector<int>path;
vector<bool>visited;
int K;
void dfs(int n,int h, int start){
if(h == K){
results.push_back(path);
return;
}
for(int i = start;i <= n ;i++){
if( (K - (int)path.size()) + i - 1 > n)break;
path.push_back(i);
dfs(n,h+1,i+1);
path.pop_back();
}
}
public:
vector<vector<int>> combine(int n, int k) {
K = k;
visited = vector<bool>(n,false);
dfs(n, 0, 1);
return results;
}
};
|
组合总和(数字可重复选取)
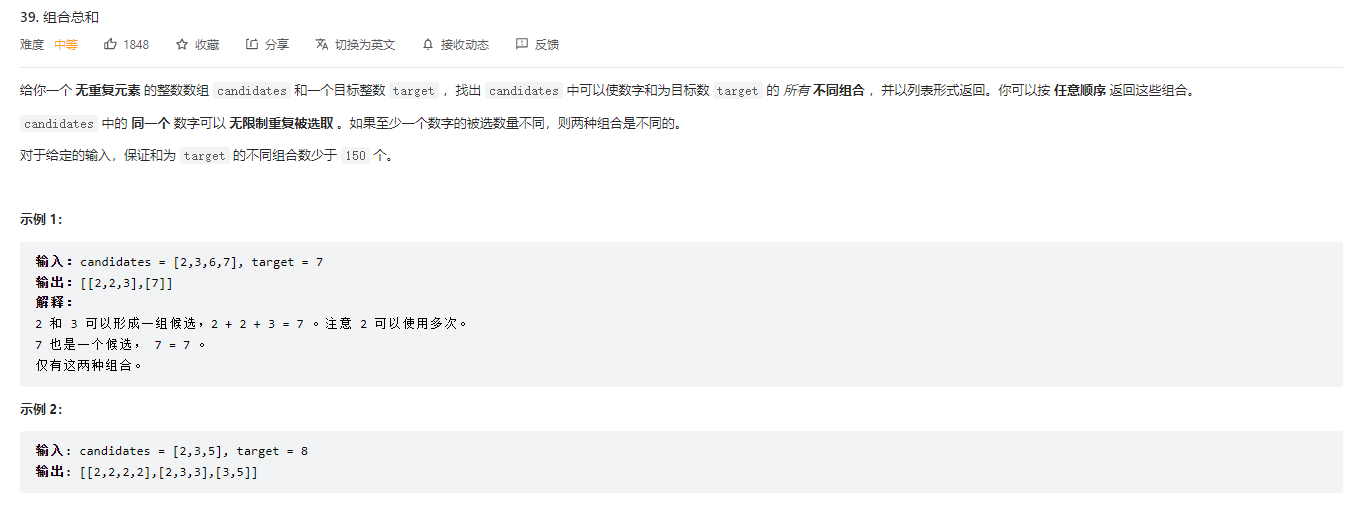
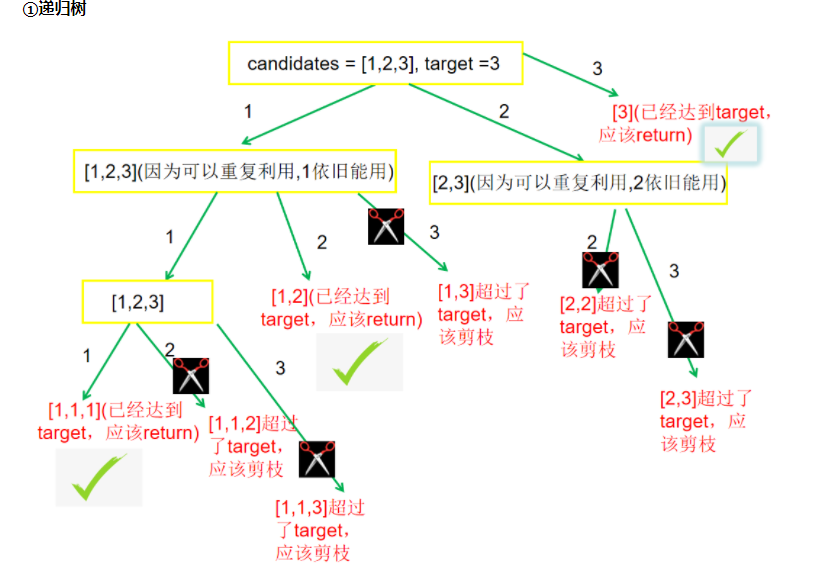
当路径总和等于 target 时候,就应该把路径加入结果集,并 return
路径和大于target时候,直接return
for(int i=start;i<nums.size();i++)
sum>target的时候可以剪枝,但是放到终止那里也可以
题中说数可以无限次被选择,那么 i 就不用 +1 。即下一层的选择列表,从自身开始。并且要更新当前状态的sum
pop_back()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
dfs(candidates,target,0,0);
return res;
}
vector<vector<int>>res;
vector<int>r;
void dfs(vector<int>& candidates, int target,int sum,int start){
if(sum == target){
res.push_back(r);
return;
}
else if(sum > target){
return;
}
else{
for(int i = start;i < candidates.size();i++){
r.push_back(candidates[i]);
dfs(candidates,target,sum+candidates[i],i);
r.pop_back();
}
}
}
};
|
组合总数2(数字不可重复选取)
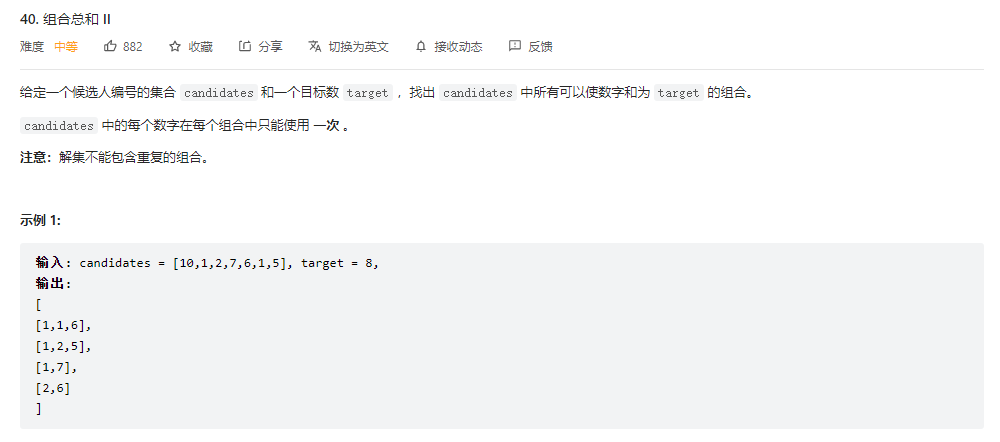
不可重复选取的问题都要先进行排列,然后对于在同一层的进行判断是否要进行剪枝操作。if(i > start && candidates[i] == candidates[i-1])continue;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
vector<vector<int>>res;
vector<int>r;
vector<bool>visited;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
dfs(candidates,target,0,0);
return res;
}
void dfs(vector<int>& candidates, int target,int sum,int start){
if(target == sum){
res.push_back(r);
return;
}
else if(sum > target){
return;
}
else{
for(int i = start;i < candidates.size();i++){
if(i > start && candidates[i] == candidates[i-1])continue;
r.push_back(candidates[i]);
dfs(candidates,target,sum+candidates[i],i+1);
r.pop_back();
}
}
}
};
|
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
vector<vector<int>>results;
vector<int>path;
vector<bool>visited;
int target;
int k;
void dfs(int h, int start, int curSum){
if(h == k){
if(curSum == target)results.push_back(path);
return;
}
for(int i = start;i <= 9;i++){
if(curSum + i > target)continue;
path.push_back(i);
dfs(h+1,i+1, curSum + i);
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum3(int k, int n) {
this->k = k;
target = n;
dfs(0, 1, 0);
return results;
}
};
|
复原IP地址
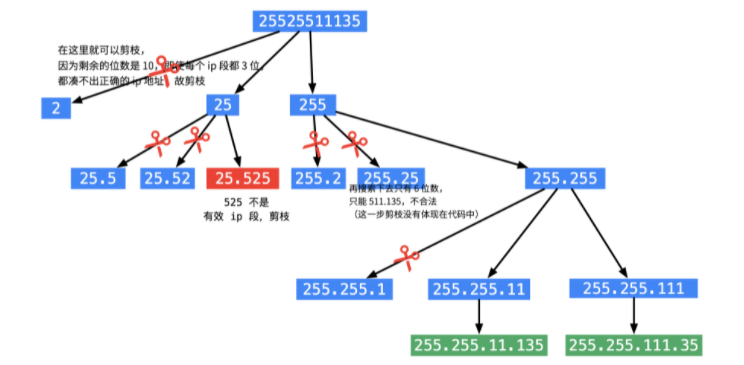
已经切分成了四段
[start,start+3)
if( start + j + (3 - strs.size() )*3 < s.size())continue;的时候可以剪枝,(即ip长度无法覆盖整个字符串)
if((tmp.size() == 3 && tmp > "255")|| (start+j>s.size())||(tmp.size()>1&&tmp[0] == '0'))continue;地址不合法的时候可以剪枝
下一层的选择列表,从这层开始地址+的这层剪的长度开始start+j。并且要更新当前状态的strs
pop_back()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
vector<string> restoreIpAddresses(string s) {
vector<string>strs;
dfs(s,strs,0);
return ans;
}
vector<string>ans;
void dfs(string s,vector<string>&strs,int start){
if(strs.size() == 4){
string tmp;
for(auto e : strs)
tmp = tmp + "." + e;
ans.push_back(tmp.substr(1));
return;
}
else{
for(int j = 1;j <= 3;j++){
string tmp = s.substr(start,j);
if( start + j + (3 - strs.size() )*3 < s.size())continue;
if((tmp.size() == 3 && tmp > "255")||
(start+j>s.size())||(tmp.size()>1&&tmp[0] == '0'))continue;
strs.push_back(s.substr(start,j));
dfs(s,strs,start+j);
strs.pop_back();
}
}
}
};
|
分割回文串
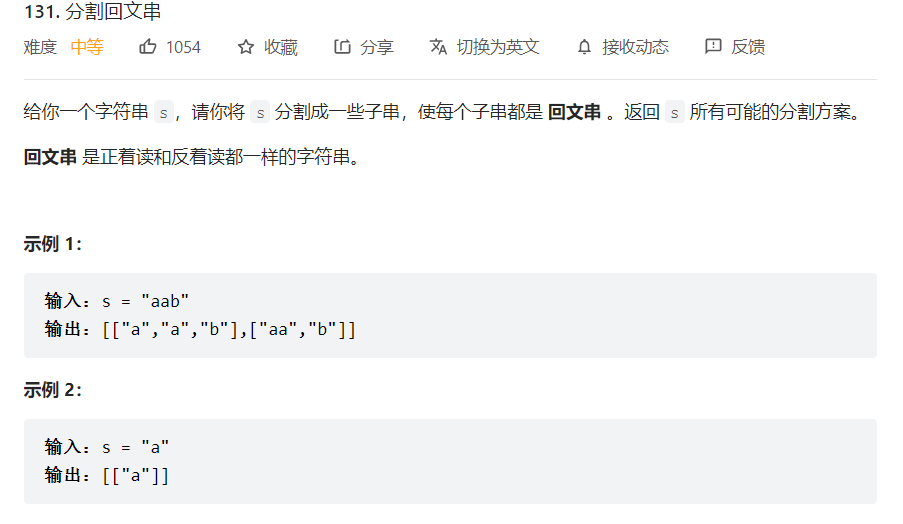
实在是感慨回溯的强大之处啊!!刚开始没有意识到使用回溯算法,更没有意识到如何切割。
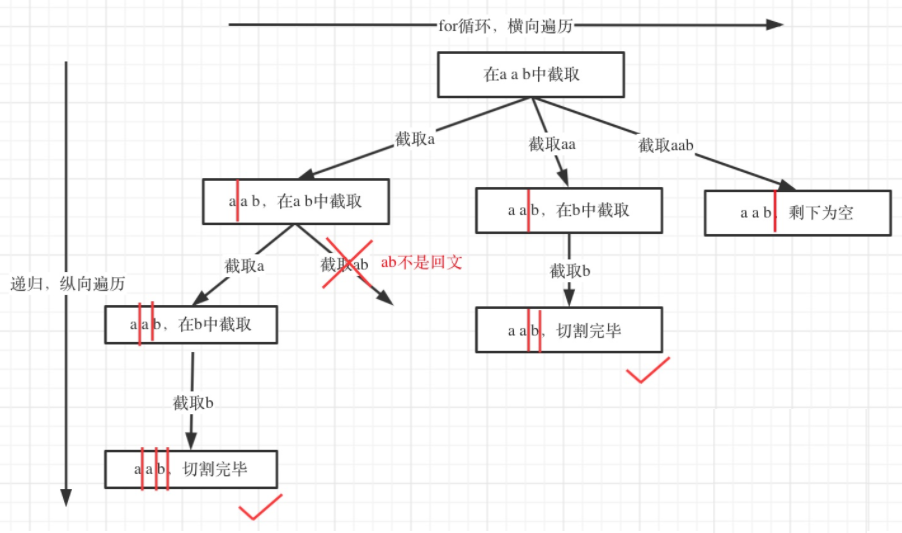
切取的指针已经到达了字符串末尾,无法继续切取
[start,start+1)~~[start,s.length()-1)若干区间都可选取
选取的区间不满足回文串的要求,那么就continue
下一层的选择列表,从这层开始地址+的这层剪的长度开始start+i。并且要更新当前状态的strs
pop_back()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
vector<vector<string>>results;
vector<string>r;
vector<vector<string>> partition(string s) {
dfs(s,0);
return results;
}
void dfs(string s,int start){
if(start == s.length()){
results.push_back(r);
return;
}
for(int i = 1;i <= s.length() - start;i++){
string tmp = s.substr(start,i);
if(!isHuiWen(tmp))continue;
else{
r.push_back(tmp);
dfs(s,start+i);
r.pop_back();
}
}
}
bool isHuiWen(string s){
for (int i = 0, j = s.length() - 1; i < j; i++, j--) {
if (s[i] != s[j]) {
return false;
}
}
return true;
}
};
|
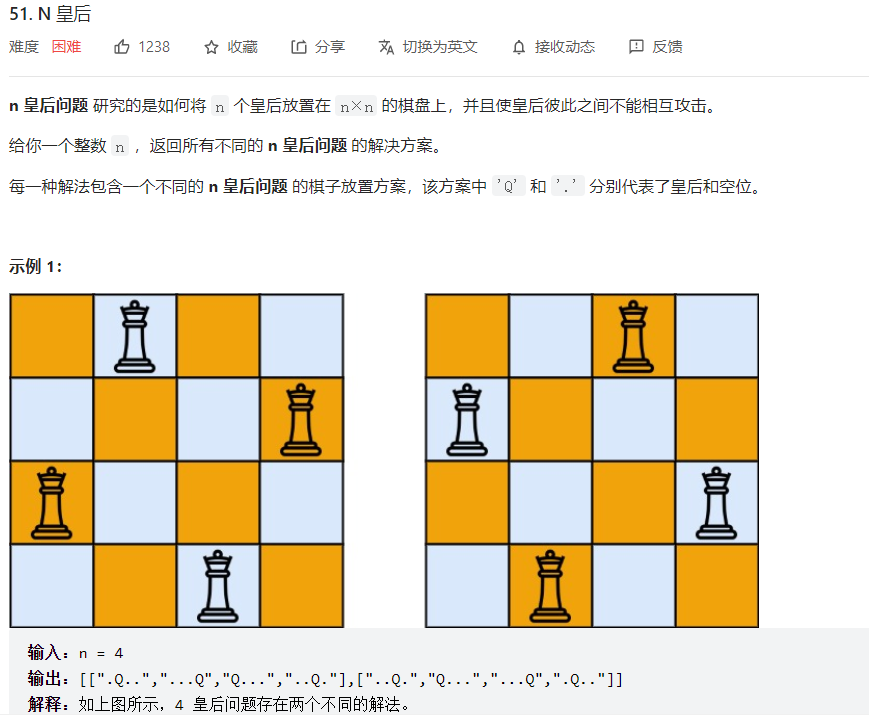
想明白递归树每一层应该存放什么,可以先暴力的思考,在稍微进行剪枝。这里每一层存放的就是这一行的皇后摆放的位置
棋盘的n行都已经填好了queen
[0,N)每一行的每一个位置都可以填
判断新填入的皇后是否会互相攻击,如果会互相攻击就剪掉
修改棋盘的当前行
将棋盘的当前行删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
int N;
vector<vector<string>>results;
vector<string>path;
bool isValid(int m,int n){
bool ret = false;
for(int i = m - 1,j = n - 1;i >= 0&&j >= 0;i--,j--){
if(path[i][j] == 'Q')ret = true;
}
for(int i = m - 1,j = n;i >= 0;i--){
if(path[i][j] == 'Q')ret = true;
}
for(int i = m - 1,j = n + 1;i >= 0&&j < N;i--,j++){
if(path[i][j] == 'Q')ret = true;
}
return ret;
}
void dfs(int h){
if(h == N){
results.push_back(path);
return;
}
for(int i = 0;i < N;i++){
if(isValid(h,i))continue;
string cur(N,'.');
cur[i] = 'Q';
path.push_back(cur);
dfs(h + 1);
path.pop_back();
}
}
public:
vector<vector<string>> solveNQueens(int n) {
N = n;
dfs(0);
return results;
}
};
|
这个递归树非常的简单
9*9数独全部都填满了
[1,9] 9个数字任选
判断新填入的数字是否会造成横竖斜存在相同值
修改数独的当前节点值
将棋盘的当前节点值删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
bool isUsed(vector<vector<char>>& board,char num,int m,int n){
for(int i = 0;i < 9;i++){
if(board[m][i] == num)return true;
}
for(int i = 0;i < 9;i++){
if(board[i][n] == num)return true;
}
for(int i = (m/3) * 3;i < (m/3) * 3+3;i++){
for(int j = (n/3) * 3;j < (n/3) * 3+3;j++){
if(board[i][j] == num)return true;
}
}
return false;
}
bool find = false;
vector<vector<char>>results;
void getNextMN(vector<vector<char>>&board,int& m,int& n){
while(m < 9 && board[m][n] != '.' ){
if(n == 8){
m++;
n = 0;
}
else n++;
}
}
void dfs(vector<vector<char>>& board,int m, int n){
getNextMN(board,m,n);
if(m == 9){
find = true;
return;
}
for(int i = 1;i <= 9;i++){
if(isUsed(board, '0' + i, m, n))continue;
board[m][n] = '0' + i;
dfs(board, m, n);
if(find)return;
board[m][n] = '.';
}
}
public:
void solveSudoku(vector<vector<char>>& board) {
dfs(board, 0, 0);
return;
}
};
|
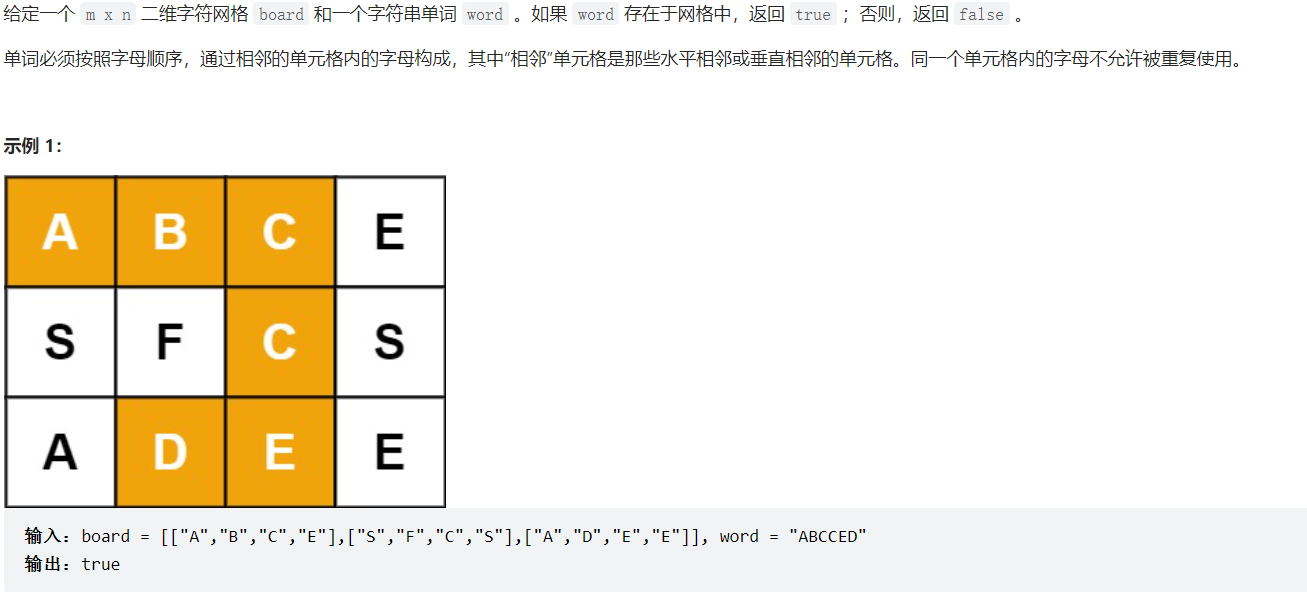
此题的一个特殊点在于除了剪枝,对当前节点应该有判断,因为dfs遍历是将栈顶元素的周边符合条件的元素也要压入栈,因此最开始的栈顶元素一定要符合标准,要避免存在第一个节点就不满足条件但是进入dfs遍历的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| int m;int n;
int des[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
bool find = false;
bool exist(vector<vector<char>>& board, string word) {
m = board.size();n = board[0].size();
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(word[0] == board[i][j])dfs(board,word,i,j,0);
if(find)return true;
}
}
return false;
}
void dfs(vector<vector<char>>& board, string word,int i,int j,int curi){
if(curi == word.length()-1){
find = true;
return;
}
char tmp = board[i][j];
board[i][j] = '#';
for(int k = 0;k < 4;k++){
int ti = i+des[k][0];
int tj = j+des[k][1];
if(ti < 0 || ti >= m || tj < 0 || tj >= n || board[ti][tj] == '#' || find || word[curi+1] != board[ti][tj]){
continue;
}
dfs(board,word,ti,tj,curi+1);
}
board[i][j] = tmp;
return;
}
|
























