前缀和其实我们很早之前就了解过的，我们求数列的和时，Sn = a1+a2+a3+…an; 此时Sn就是数列的前 n 项和。例 S5 = a1 + a2 + a3 + a4 + a5; S2 = a1 + a2。所以我们完全可以通过 S5-S2 得到 a3+a4+a5 的值，这个过程就和我们做题用到的前缀和思想类似。我们的前缀和数组里保存的就是前 n 项的和。见下图

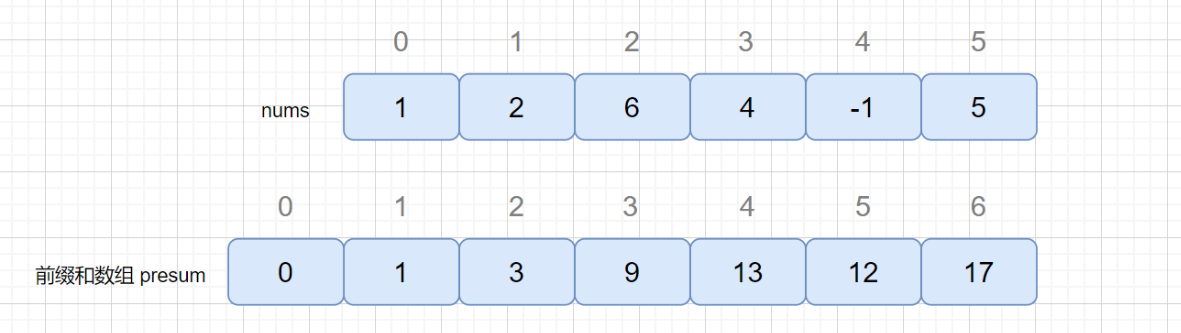
image-20220418154438036

**我们通过前缀和数组保存前 n 位的和(不包含下标n自身这位)**，presum[1]保存的就是 nums 数组中前 1 位的和，也就是 presum[1] = nums[0], presum[2] = nums[0] + nums[1] = presum[1] + nums[1]. 依次类推，所以我们通过前缀和数组可以轻松得到每个区间的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        int len = nums.size();
        vector<int>preSum(len + 1,0);
        int sum = 0;
        for(int i = 0;i < len;i++){
            sum += nums[i];
            preSum[i + 1] = preSum[i] + nums[i];
        }
        for(int i = 0;i < len;i++){
            if(sum - preSum[i] - nums[i] == preSum[i])return i;
        }
        return -1;
    }
};

724. 寻找数组的中心下标

image-20220418154307757

1
2
3
4
5
6
7
8
9
10
11
12
13
int pivotIndex(vector<int>& nums) {
    int len = nums.size();
    vector<int>preSum(len + 1,0);
    int sum = 0;
    for(int i = 0;i < len;i++){
        sum += nums[i];
        preSum[i + 1] = preSum[i] + nums[i];
    }
    for(int i = 0;i < len;i++){
        if(sum - preSum[i] - nums[i] == preSum[i])return i;
    }
    return -1;
}

560. 和为 K 的子数组

image-20220418153412984

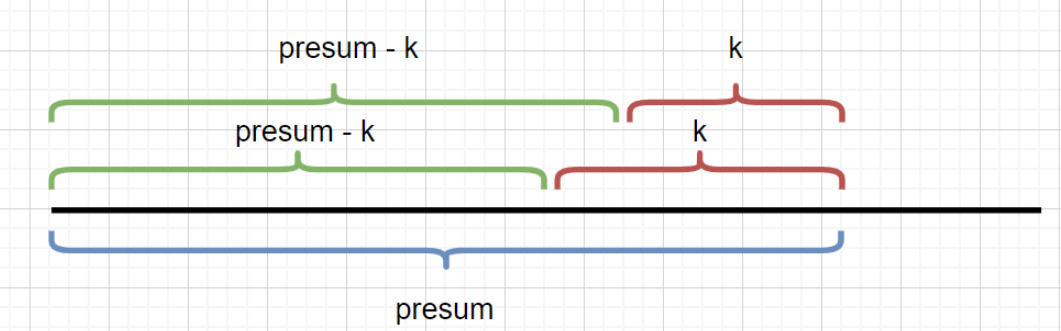
思考为什么我们只要查看是否含有 presum - k ，并获取到presum - k 出现的次数就行呢？见下图，所以我们完全可以通过 presum - k的个数获得 k 的个数

image-20220418153528804

preSum是我当前遍历到的节点的前缀总和，只需查看hash表内preSum-k是否存在以及hash值具体多少，每遍历一次将hash表更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int cnt = 0;
        int len = nums.size();
        int preSum = 0;
        unordered_map<int,int>hash;
        
        //细节，这里需要预存前缀和为 0 的情况，会漏掉前几位就满足的情况
        //例如输入[1,1,0]，k = 2 如果没有这行代码，则会返回0,漏掉了1+1=2，和1+1+0=2的情况
        //输入：[3,1,1,0] k = 2时则不会漏掉
        hash[0] = 1;
        for(auto n : nums){
            preSum += n;
            if(hash.count(preSum - k) > 0){
                cnt += hash[preSum - k];
            }
            hash[preSum]++;
        }
        return cnt;
    }
};

1248. 统计「优美子数组」

image-20220418155747393

上个题目我们是求和为 K 的子数组，这个题目是让我们求 恰好有 k 个奇数数字的连续子数组，这两个题几乎是一样的，上个题中我们将前缀区间的和保存到哈希表中，这个题目我们只需将前缀区间的奇数个数保存到区间内即可，只不过将 sum += x 改成了判断奇偶的语句，见下图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int numberOfSubarrays(vector<int>& nums, int k) {
        int len = nums.size();
        int cnt = 0;
        int preSum = 0;
        unordered_map<int,int>hash;
        hash[0] = 1;
        for(auto&n : nums){
            preSum += (n&1);
            if(hash.count(preSum - k)>0){
                cnt += hash[preSum - k];
            }
            hash[preSum]++;
        }
        return cnt;
    }
};

974. 和可被 K 整除的子数组

image-20220418161829703

我们在之前的例子中说到，presum[j+1] - presum[i] 可以得到 nums[i] + nums[i+1]+…. nums[j]，也就是[i,j]区间的和。

那么我们想要判断区间 [i,j] 的和是否能整除 K，也就是上图中紫色那一段是否能整除 K，那么我们只需判断

(presum[j+1] - presum[i] ) % k 是否等于 0 即可，

我们假设 (presum[j+1] - presum[i] ) % k == 0；则

presum[j+1] % k - presum[i] % k == 0;

presum[j +1] % k = presum[i] % k ;

我们 presum[j +1] % k 的值 key 是已知的，则是当前的 presum 和 k 的关系，我们只需要知道之前的前缀区间里含有相同余数 （key）的个数。则能够知道当前能够整除 K 的区间个数。见下图

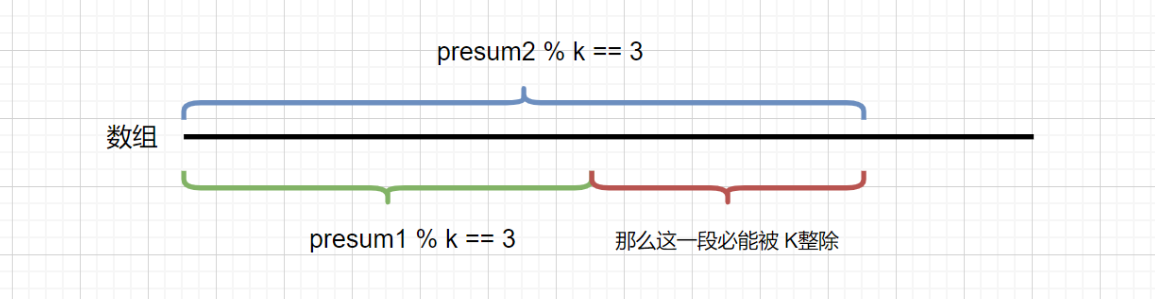
image-20220418161814878

我们看到代码中有一段代码是这样的

int key = (presum % K + K) % K;
这是为什么呢？不能直接用 presum % k 吗？

这是因为当我们 presum 为负数时，需要对其纠正。纠正前(-1) %2 = (-1)，纠正之后 ( (-1) % 2 + 2) % 2=1 保存在哈希表中的则为 1.则不会漏掉部分情况，例如输入为 [-1,2,9],K = 2如果不对其纠正则会漏掉区间 [2] 此时 2 % 2 = 0，符合条件，但是不会被计数。

那么这个题目我们可不可以用数组，代替 map 呢？当然也是可以的，因为此时我们的哈希表存的是余数，余数最大也只不过是 K-1所以我们可以用固定长度 K 的数组来模拟哈希表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int>hash;
        hash[0] = 1;
        int cnt = 0;
        int preSum = 0;
        for(auto &n : nums){
            preSum += n;
            int key = (preSum%k + k)%k;
            if(hash.count(key) > 0){
                cnt += hash[key];
            }
            hash[key]++;
        }
        return cnt;
    }
};

523. 连续的子数组和

image-20220418164340066

这个题目算是对刚才那个题目的升级，前半部分是一样的，都是为了让你找到能被 K 整除的子数组，但是这里加了一个限制，那就是子数组的大小至少为 2，那么我们应该怎么判断子数组的长度呢？我们可以根据索引来进行判断，见下图。

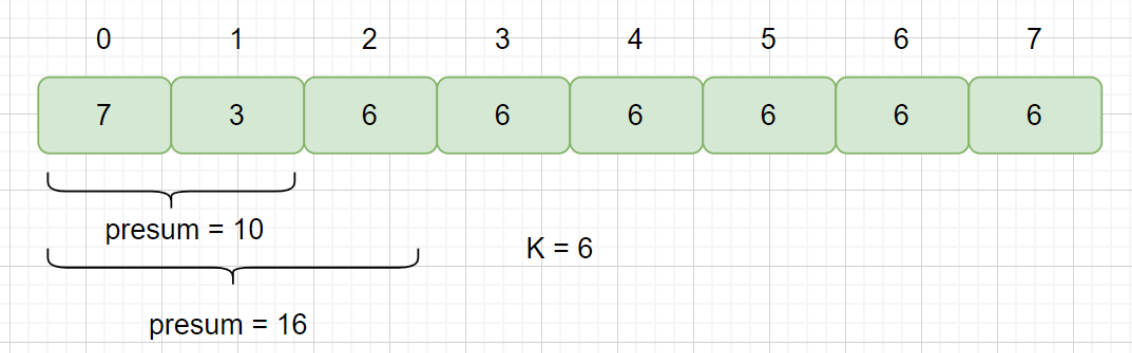
image-20220418164416867

此时我们 K = 6, presum % 6 = 4 也找到了相同余数的前缀子数组 [0,1] 但是我们此时指针指向为 2，我们的前缀子区间 [0,1]的下界为1，所以 2 - 1 = 1，但我们的中间区间的长度小于2，所以不能返回 true，需要继续遍历，那我们有两个区间[0,1],[0,2]都满足 presum % 6 = 4，那我们哈希表中保存的下标应该是 1 还是 2 呢？我们保存的是1，如果我们保存的是较大的那个索引，则会出现下列情况，见下图。

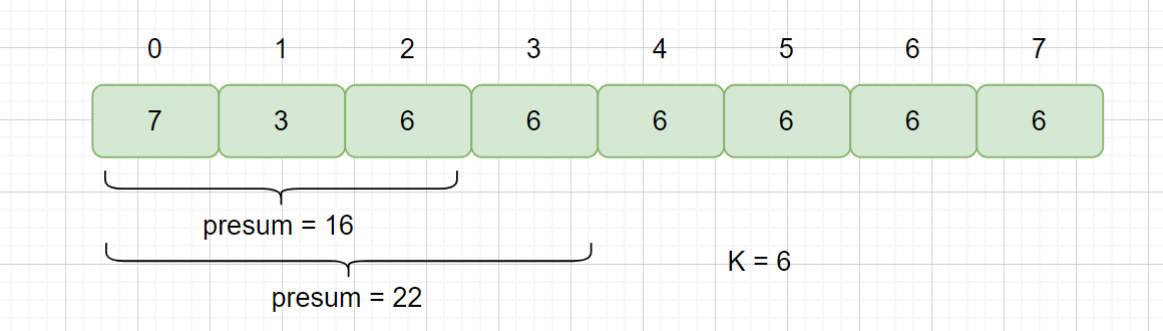
image-20220418164435202

此时，仍会显示不满足子区间长度至少为 2 的情况，仍会继续遍历，但是我们此时的 [2,3]区间已经满足该情况，返回 true，所以我们往哈希表存值时，只存一次，即最小的索引即可。下面我们看一下该题的两个细节

细节1：我们的 k 如果为 0 时怎么办，因为 0 不可以做除数。所以当我们 k 为 0 时可以直接存到数组里，例如输入为 [0,0] , K = 0 的情况

细节2：另外一个就是之前我们都是统计个数，value 里保存的是次数，但是此时我们加了一个条件就是长度至少为 2，保存的是索引，所以我们不能继续 map.put(0,1)，应该赋初值为 map.put(0,-1)。这样才不会漏掉一些情况，例如我们的数组为[2,3,4],k = 1,当我们 map.put(0,-1) 时，当我们遍历到 nums[1] 即 3 时，则可以返回 true，因为 1-（-1）= 2，5 % 1=0 , 同时满足。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        unordered_map<int,int>hash;
        hash[0] = -1;
        long long preSum = 0;
        
        for(int i = 0;i < nums.size();i++){
            preSum += nums[i];
            int key = k == 0?preSum : preSum%k;
            if(hash.count(key) > 0){
                if(i - hash[key] >= 2)return true;
                else continue;
            }
            hash[key] = i;
        }
        return false;
    }
};

437. 路径总和 III

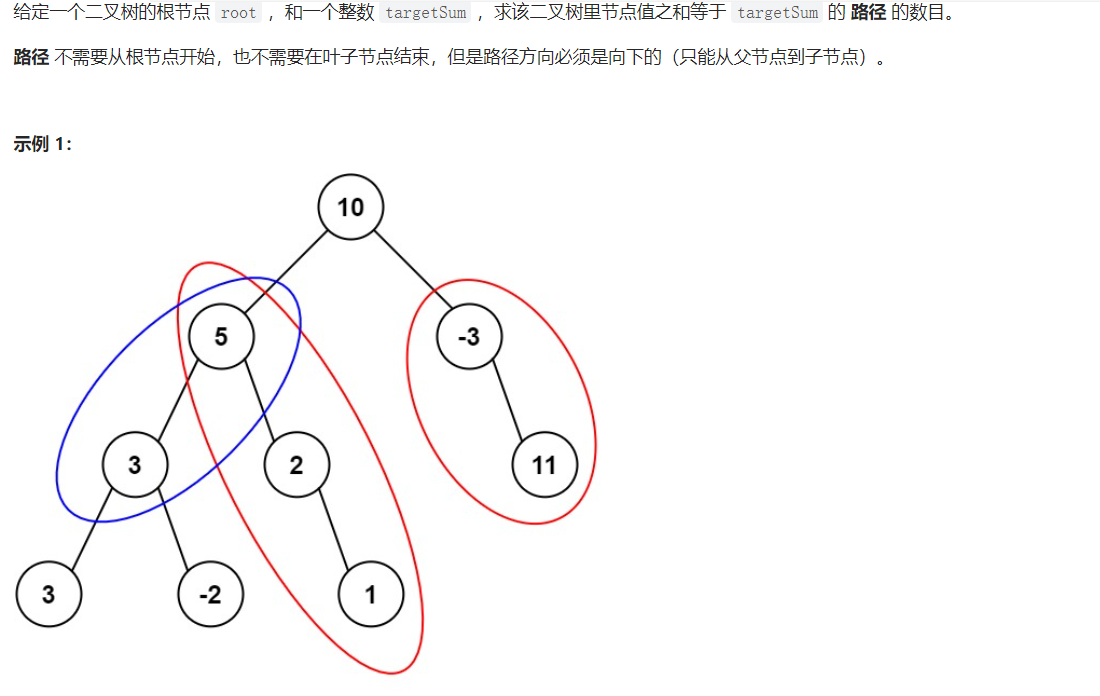
image-20220418170902079

前序遍历加回溯，简单解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    unordered_map<int,int>hash;
    int cnt = 0;
    long long target;
public:
    int pathSum(TreeNode* root, int targetSum) {
        target = targetSum;
        hash[0] = 1;
        dfs(root,0);
        return cnt;
    }
    void dfs(TreeNode* root,long long preSum){
        if(root == nullptr)return;
        preSum += root->val;
        if(hash[preSum - target] > 0){
            cnt += hash[preSum - target];
        }
        hash[preSum]++;
        dfs(root->left,preSum);
        dfs(root->right,preSum);
        hash[preSum]--;
    }
};