树的遍历

144. 二叉树的前序遍历(迭代)

根左右

借助栈实现，注意空节点不应该入栈，每次取出栈顶元素就是先序结果，注意每一次循环中应该让左孩子位于栈顶，于是呢就先压入右孩子，再压入左孩子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> preorderTraversal(TreeNode* root) {
    stack<TreeNode*>st;
    vector<int>results;
    if(root == nullptr)return results;
    st.push(root);
    while(!st.empty()){
        TreeNode* cur = st.top();
        st.pop();
        results.push_back(cur->val);					//根，每次取出的是栈顶元素根
        if(cur->right != nullptr)st.push(cur->right);	//先入右孩子，右孩子在栈底部
        if(cur->left != nullptr)st.push(cur->left);		//再入左孩子，这样左孩子就是在栈顶
    }
    return results;
}

145. 二叉树的后序遍历

左右根，因为每次从栈中取得的元素是根，因此迭代顺序就是根左右或者根右左，而我们要求左右根，只需要求出根右左，然后将结果翻转reverse一下即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> postorderTraversal(TreeNode* root) {
    stack<TreeNode*>st;
    vector<int>results;
    if(root == nullptr)return results;
    st.push(root);
    while(!st.empty()){
        TreeNode* cur = st.top();
        st.pop();
        results.push_back(cur->val);                    //根，每次取出的是栈顶元素根
        if(cur->left != nullptr)st.push(cur->left);		//先入左孩子，左孩子在栈底部
        if(cur->right != nullptr)st.push(cur->right);	//再入右孩子，这样右孩子就是在栈顶
    }
    //最终结果根右左，最后reverse翻转一下得到左右根即可
    reverse(results.begin(),results.end());
    return results;
}

94. 二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<TreeNode*> st;
    TreeNode* cur = root;
    while (cur != NULL || !st.empty()) {
        if (cur != NULL) { // 指针来访问节点，访问到最底层
            st.push(cur); // 将访问的节点放进栈
            cur = cur->left;                // 左
        } else {
            cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
            st.pop();
            result.push_back(cur->val);     // 中
            cur = cur->right;               // 右
        }
    }
    return result;
}

102. 二叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>>results;
    if(root == nullptr)return results;
    queue<TreeNode*>q;
    q.push(root);
    while(!q.empty()){
        int size = q.size();
        vector<int>tmp;
        while(size--){
            TreeNode* cur = q.front();
            q.pop();
            tmp.push_back(cur->val);
            if(cur->left != nullptr)q.push(cur->left);
            if(cur->right != nullptr)q.push(cur->right);
        }
        results.push_back(tmp);
    }
    return results;
}

树

124. 二叉树中的最大路径和

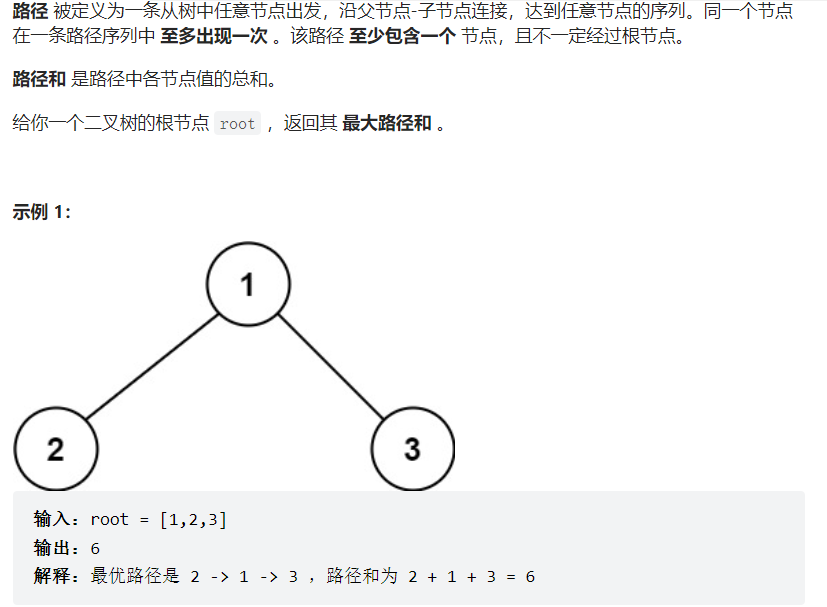
image-20220412180934478

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result = INT_MIN;
    int maxPathSum(TreeNode* root) {
        maxUp(root);
        return result;
    }
    //maxUp返回能够给父节点提供的最大贡献值
    int maxUp(TreeNode* root){
        //递归出口
        if(root == nullptr)return 0;
        //取得左右子树的贡献
        int left = maxUp(root->left);
        int right = maxUp(root->right);
        //对于二叉树中每一个节点都可以从中更新result最大值
        result = max(result,left+right+root->val);
        
        //根据 当前节点的左右子树贡献+自己节点值 为当前节点能给父节点提供的贡献
        int maxu = max(left,right) + root->val;
        //壮士割腕，如果能给上面提供的贡献小于0,干脆别提供了返回个0
        maxu = max(0,maxu);
        return maxu;
    }
};

101. 对称二叉树

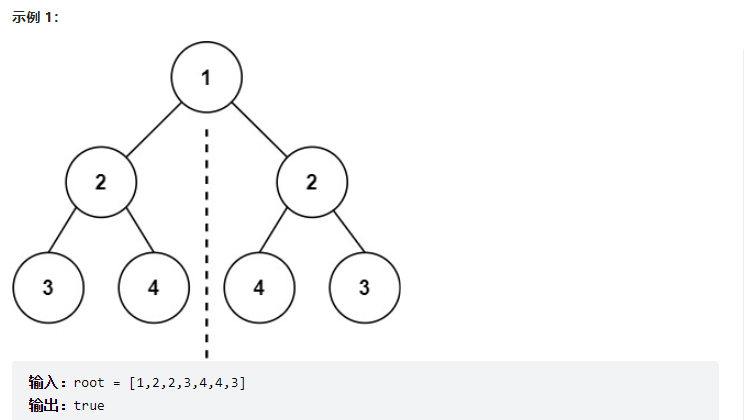
image-20220509172346142

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return isSymmetric(root->left,root->right); 
    }
    bool isSymmetric(TreeNode* left,TreeNode* right){
        if(left == nullptr && right == nullptr)return true;
        else if(left == nullptr)return false;
        else if(right == nullptr)return false;
        else {
            return left->val == right->val && isSymmetric(left->left, right->right) 
                &&isSymmetric(left->right, right->left);
        }
    }
};

104. 二叉树的最大深度

二叉树的深度应该先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。因此这是一个后序遍历。

1
2
3
4
5
6
7
int maxDepth(TreeNode* root) {
    if(root == nullptr)return 0;
    int l = maxDepth(root->left);   //左
    int r = maxDepth(root->right);  //右
    int depth = max(l,r) + 1;       //根
    return depth;
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明: 叶子节点是指没有子节点的节点。

1
2
3
4
5
6
7
8
9
int minDepth(TreeNode* root) {
    if(root == nullptr)return 0;
    int minl;
    if(root->left == nullptr && root->right == nullptr)minl = 0;
    else if(root->left == nullptr)minl = minDepth(root->right);
    else if(root->right == nullptr)minl = minDepth(root->left);
    else minl = min(minDepth(root->left),minDepth(root->right));
    return minl + 1; 
}

105. 从前序与中序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int len = preorder.size();
        return buildTree(preorder,inorder,0,len-1,0,len-1);
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder,int l1, int r1,int l2, int r2) {
        if(r1 < l1)return nullptr;//注意r1<l1表示没有节点，应该要返回nullptr
        if(r1 == l1)return new TreeNode(preorder[l1]);//r1 == l1说明仅此一个节点，应当返回这一个节点即可
        
        TreeNode* rt = new TreeNode(preorder[l1]);
        int len = 0;
        while(inorder[l2+len] != rt->val)len++;

        rt->left = buildTree(preorder,inorder,l1+1,l1+len,l2,l2+len-1);
        rt->right = buildTree(preorder, inorder,l1+len+1,r1,l2+len+1,r2);
        return rt;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
string buildTree(string preorder, string inorder, int l1, int r1, int l2, int r2) {
    if (r1 < l1)return "";
    if (r1 == l1)return string(1,preorder[l1]);

    char rt = preorder[l1];
    int len = 0;
    while (inorder[l2 + len] != rt)len++;
    

    string left = buildTree(preorder, inorder, l1 + 1, l1 + len, l2, l2 + len - 1);
    string right = buildTree(preorder, inorder, l1 + len + 1, r1, l2 + len + 1, r2);
    return left + right + string(1,rt);
}

654. 构建最大二叉树

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

  • 二叉树的根是数组中的最大元素。
  • 左子树是通过数组中最大值左边部分构造出的最大二叉树。
  • 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

654.最大二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    return construct(nums,0,static_cast<int>(nums.size()) - 1);
}
TreeNode* construct(vector<int>& nums,int l,int r){
    if(l > r)return nullptr;				//这里不能忽略，没有节点应该返回nullptr
    if(l == r)return new TreeNode(nums[l]);	//仅一个节点直接返回就可以

    int maxi = l;
    for(int i = l;i <= r;i++){
        if(nums[i] > nums[maxi])maxi = i;
    }
    TreeNode* root = new TreeNode(nums[maxi]);
    root->left = construct(nums,l,maxi-1);
    root->right = construct(nums,maxi+1,r);
    return root;
}

110. 平衡二叉树

如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。

1
2
3
4
5
6
7
8
9
10
int getHeight(TreeNode* root){
    if(root == nullptr)return 0;
    int l = getHeight(root->left);
    int r = getHeight(root->right);
    if(l == -1 || r == -1 || abs(l-r) > 1)return -1;
    else return max(l,r) + 1;
}
bool isBalanced(TreeNode* root) {
    return getHeight(root) != -1;
}

222. 完全二叉树的节点个数

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int countNodes(TreeNode* root) {
    if(root == nullptr)return 0;

    TreeNode* cur = root;
    int ldepth = 0,rdepth = 0;
    while(cur != nullptr){
        cur = cur->left;
        ldepth++;
    }
    cur = root;
    while(cur != nullptr){
        cur = cur->right;
        rdepth++;
    }
    if(ldepth == rdepth)return pow(2,ldepth) - 1;
    else return 1 + countNodes(root->left) + countNodes(root->right);
}

226. 翻转二叉树

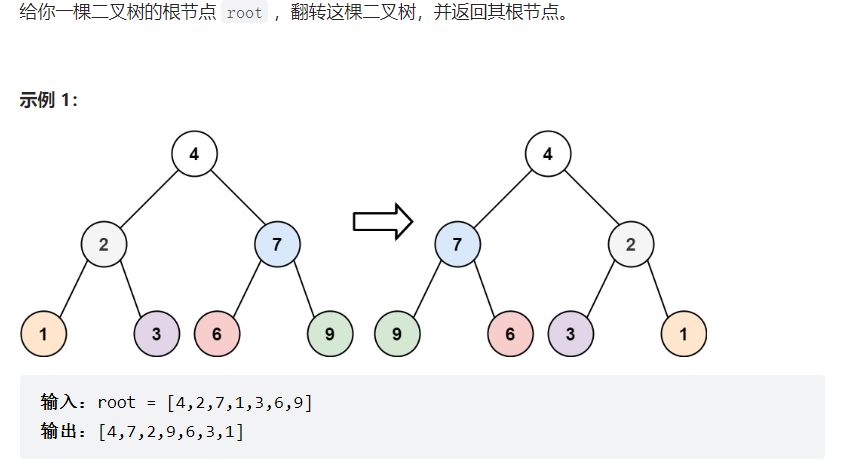
image-20220509171233697

1
2
3
4
5
6
7
TreeNode* invertTree(TreeNode* root) {
    if(root == nullptr)return root;
    swap(root->left,root->right);
    if(root->left!=nullptr)invertTree(root->left);
    if(root->right!=nullptr)invertTree(root->right);
    return root;
}

二叉搜索树

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。

  • 节点的右子树只包含 大于 当前节点的数。

  • 所有左子树和右子树自身必须也是二叉搜索树。

解答：

根据二叉搜索树的特性,可知中序遍历的结果是有序的.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    long long pre = LONG_MIN;
    bool ret = true;
public:
    bool isValidBST(TreeNode* root) {
        inorder(root);
        return ret;
    }
    void inorder(TreeNode* root) {
        if(root == nullptr)return;
        if(ret == false)return;
        inorder(root->left);
        if(root->val <= pre)ret = false;
        else pre = root->val;
        inorder(root->right);
    }
};

剑指 Offer 33. 判断是否为二叉搜索树的后序遍历序列

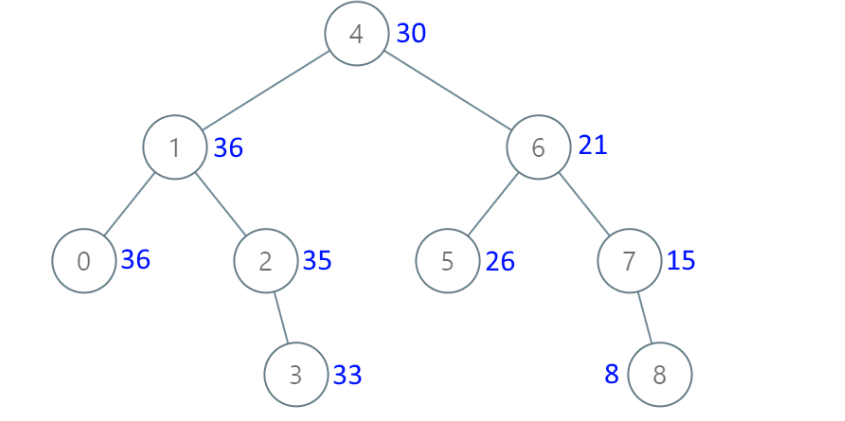
如果这题说的是判断该数组是不是某二叉搜索树的中序遍历结果，那么这道题就非常简单了，因为二叉搜索树的中序遍历结果一定是有序的，我们只需要判断数组是否有序就行了。但这道题要判断的是不是某二叉搜索树的后序遍历结果，这样就有点难办了。

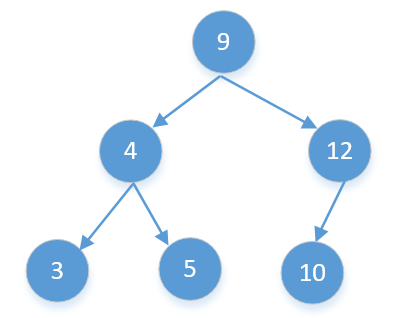
比如下面这棵二叉树，他的后续遍历是

[3，5，4，10，12，9]

image.png

我们知道后续遍历的最后一个数字一定是根节点，所以数组中最后一个数字9就是根节点，我们从前往后找到第一个比9大的数字10，那么10后面的[10，12]（除了9）都是9的右子节点，10前面的[3，5，4]都是9的左子节点，后面的需要判断一下，如果有小于9的，说明不是二叉搜索树，直接返回false。然后再以递归的方式判断左右子树。

[3，5，4，10，12，9]如此划分，和前面的题差不多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:  
    bool verifyPostorder(vector<int>& postorder) {
        return verifyPostorder(postorder,0,postorder.size() - 1);
    }
    bool verifyPostorder(vector<int>& postorder,int left,int right) {
        if(right - left <= 1)return true;//如果少于或等于两个节点，必定可以构成e

        int rt = postorder[right];
        int len = 0;
        while(postorder[left+len] < rt)len++;

        int cur = left + len;
        while(cur < right){
            if(postorder[cur++] < rt)return false;
        }

        return verifyPostorder(postorder,left,left+len-1)
            &&verifyPostorder(postorder,left+len,right-1);
    }
};

剑指 Offer 36. 二叉搜索树与双向链表

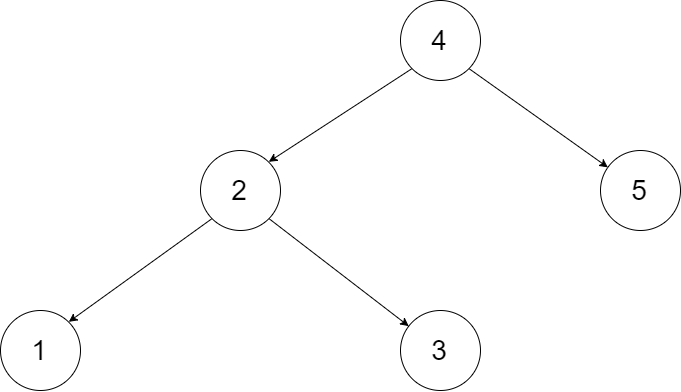
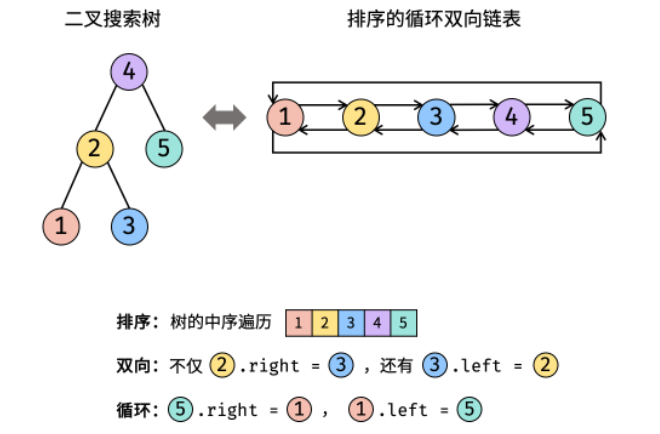
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

img

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

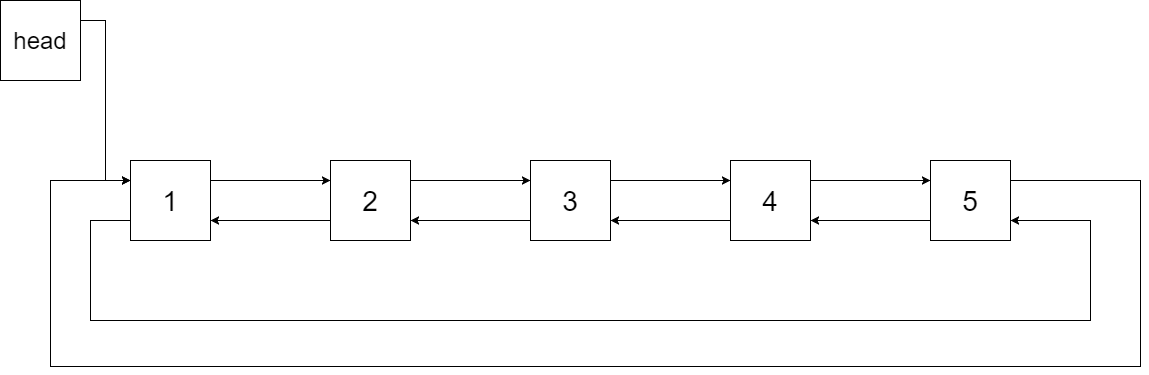
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

img

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

这题注意双向链表顺序是二叉搜索树的中序遍历

image-20220507174259683

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    Node* pre;
public:
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr)return nullptr;
        dfs(root);
        Node* head = root; 
        while(head->left != nullptr)head = head->left;
        Node* tail = root;
        while(tail->right != nullptr)tail = tail->right;
        head->left = tail;
        tail->right = head;
        return head;
    }

    void dfs(Node* cur){
        if(cur == nullptr)return;
        dfs(cur->left);

        if(pre == nullptr){
            cur->left = pre;
        }
        else {
            pre->right = cur;
            cur->left = pre;
        }
        pre = cur;
        dfs(cur->right);
    }
};

剑指 Offer 54. 二叉搜索树的第k大节点

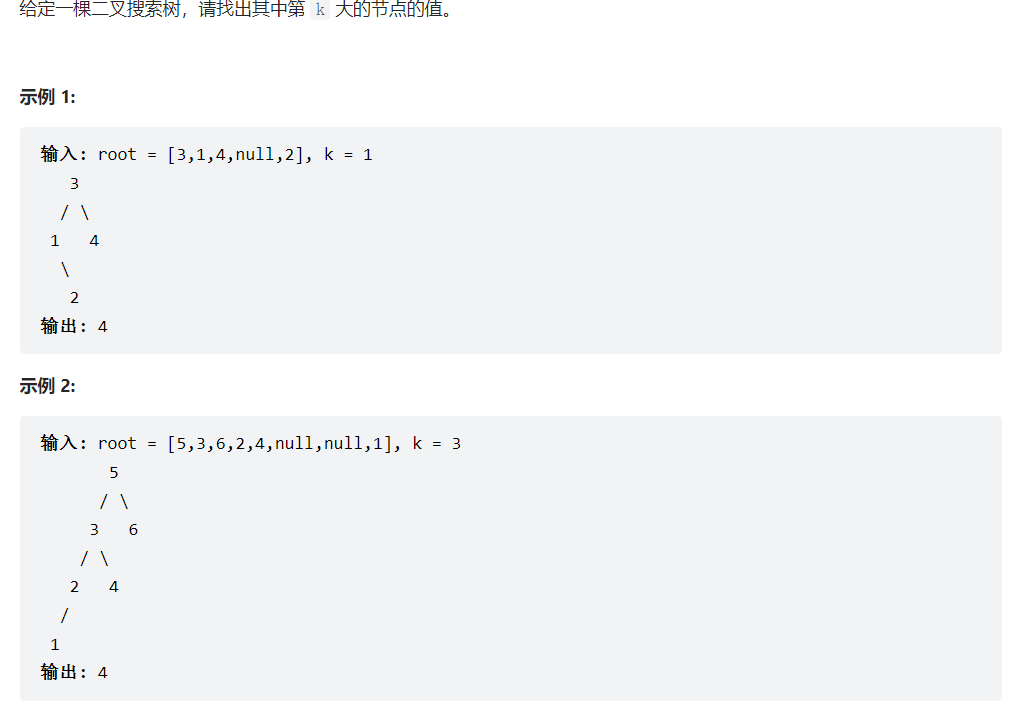
image-20220509165054005

请务必记住二叉搜索树的特性，中序遍历就是从小到大，因此这题肯定需要中序遍历，但是这题是寻找第k大的节点，那么考虑右根左这样的遍历顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int result;
    int cnt;
    int kthLargest(TreeNode* root, int k) {
        cnt = k;
        dfs(root);
        return result;
    }
    void dfs(TreeNode* cur){
        if(cur == nullptr)return;
        dfs(cur->right);
        cnt--;
        if(cnt == 0){
            result = cur->val;
            return;
        }
        dfs(cur->left);
    }
};

538. 把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。

  • 节点的右子树仅包含键 大于 节点键的节点。

  • 左右子树也必须是二叉搜索树。

image-20220512115802187

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    int sum = 0;
public:
    TreeNode* convertBST(TreeNode* root) {
        dfs(root);
        return root;
    }
    void dfs(TreeNode* root){
        if(root == nullptr)return;
        dfs(root->right);
        sum += root->val;
        root->val = sum;
        dfs(root->left);
    }
};

树+回溯

回溯模板

树的回溯模板和图的回溯模板略有不同

1.确定递归终止条件

那么什么时候算是找到了叶子节点？ 是当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。

叶子节点终止条件是：

1
2
3
if (cur->left == nullptr && cur->right == nullptr) {	//而不是粗暴的if(cur == nullptr)
    终止处理逻辑
}

2.单层递归的逻辑

因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。

1
path.push_back(cur->val);

然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。

所以递归前要加上判断语句，下面要递归的节点是否为空，如下

1
2
3
4
5
6
if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}

此时还没完，递归完，要做回溯啊，因为path 不能一直加入节点，它还要删节点，然后才能加入新的节点。

那么回溯要怎么回溯呢，一些同学会这么写，如下：

1
2
3
4
5
6
7
if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}
path.pop_back();

这个回溯就要很大的问题，我们知道，回溯和递归是一一对应的，有一个递归，就要有一个回溯，这么写的话相当于把递归和回溯拆开了， 一个在花括号里，一个在花括号外。

所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！

那么代码应该这么写：

1
2
3
4
5
6
7
8
9
10
if (cur->left) {
    path.push_back(cur->val);
    traversal(cur->left, path, result);
    path.pop_back(); // 回溯
}
if (cur->right) {
    path.push_back(cur->val);
    traversal(cur->right, path, result);
    path.pop_back(); // 回溯
}

什么时候递归需要返回值？

  • 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是113. 路径总和 II）
  • 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
  • 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（112. 路径总和）

112. 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

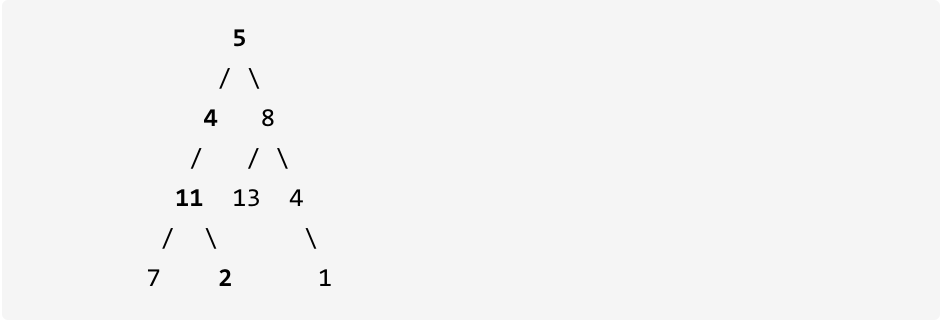
示例: 给定如下二叉树，以及目标和 sum = 22，

112.路径总和1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)return false;
        return dfs(root,targetSum);
    }
    bool dfs(TreeNode* cur, int targetSum){
        if(cur->left == nullptr && cur->right == nullptr){//叶子节点
            if(targetSum == cur->val)return true;
            else return false;
        }

        if(cur->left != nullptr){
            if(dfs(cur->left,targetSum - cur->val))return true;
        }
        if(cur->right != nullptr){
            if(dfs(cur->right,targetSum - cur->val))return true;
        }
        return false;
    }
};

257. 二叉树的所有路径

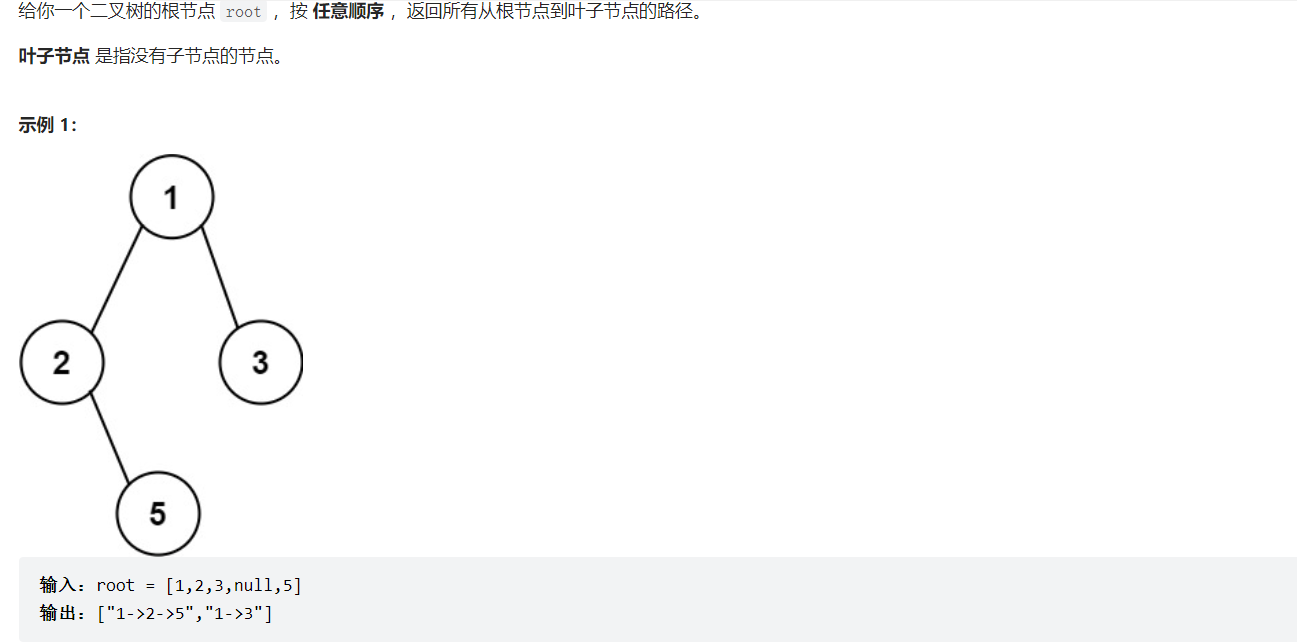
image-20220504170957099

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<string>results;
vector<string> binaryTreePaths(TreeNode* root) {
    if(root != nullptr)dfs(root,"");
    return results;
}
void dfs(TreeNode* cur,string path){
    if(cur->left == nullptr&& cur->right == nullptr){
        results.push_back(path+to_string(cur->val));
    }
    if(cur->left != nullptr){
        dfs(cur->left,path + to_string(cur->val) + "->");
    }
    if(cur->right != nullptr){
        dfs(cur->right,path + to_string(cur->val) + "->");
    }
}

113. 路径总和 II

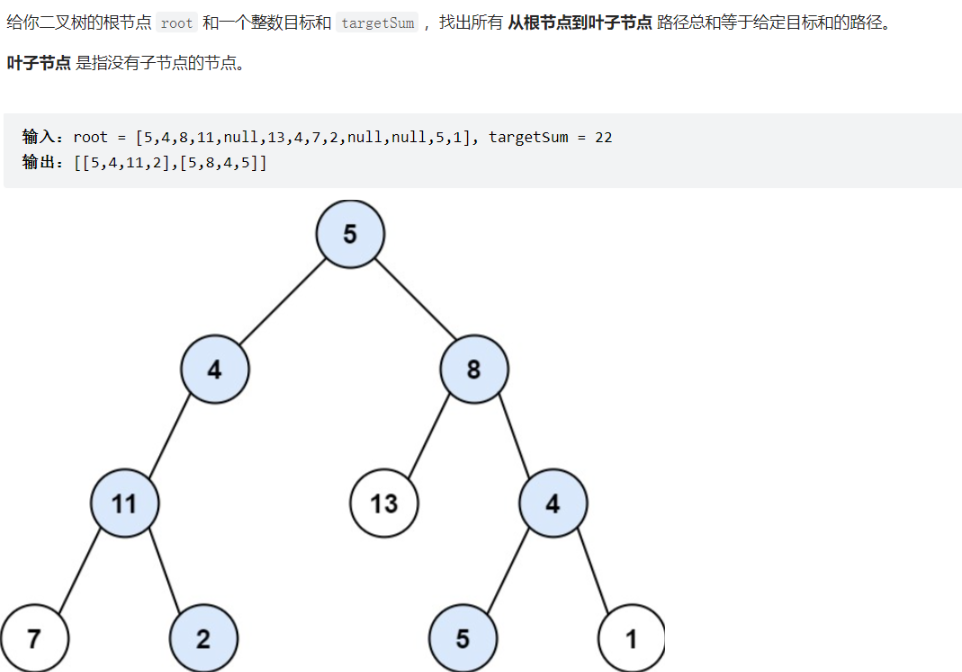
image-20220504172725154

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>>results;
    vector<int>path;
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        if(root != nullptr)dfs(root,target);
        return results;
    }
    void dfs(TreeNode* cur,int target){
        if(cur->left == nullptr && cur->right == nullptr){
            path.push_back(cur->val);			//回溯begin
            if(target == cur->val)results.push_back(path);
            path.pop_back();					//回溯end
            return;
        }
        if(cur->left != nullptr){
            path.push_back(cur->val);			//回溯begin
            dfs(cur->left, target-cur->val);
            path.pop_back();					//回溯end
        }
        if(cur->right != nullptr){
            path.push_back(cur->val);			//回溯begin
            dfs(cur->right, target-cur->val);
            path.pop_back();					//回溯end
        }
    }
};

236. 二叉树的最近公共祖先

  1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。
  2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
  3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。
1
2
3
4
5
6
7
8
9
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(root == nullptr || root == p || root == q)return root;
    TreeNode* left = lowestCommonAncestor(root->left,p,q);
    TreeNode* right = lowestCommonAncestor(root->right,p,q);
    if(left != nullptr && right != nullptr)return root;
    else if(left == nullptr)return right;
    else if(right == nullptr)return left;
    else return nullptr;    //(left == nullptr && right == nullptr)
}