剑指 Offer 03. 数组中重复的数字

image-20220427095055235

方法一：哈希表，较为简单

方法二：原地置换

  1. 所谓原地交换，就是如果发现这个坑里面的萝卜不是这个坑应该有的萝卜，就看看你是哪家的萝卜，然后把你送到哪家，再把你家里现在那个萝卜拿回来。
  2. 拿回来之后，再看看拿回来的这个萝卜应该是属于哪家的，再跟哪家交换。
  3. 就这样交换萝卜，直到想把这个萝卜送回它家的时候，发现人家家里已经有了这个萝卜了（双胞胎啊），那这个萝卜就多余了，就把这个萝卜上交给国家。
1
2
3
4
5
6
7
8
9
10
11
int findRepeatNumber(vector<int>& nums) {
    int len = nums.size();
    for(int i = 0;i < len;i++){
        while(nums[i] != i){   				//只要没有填到相应的坑就一直换
            int tmp = nums[i];				//看看你是哪家萝卜
            if(nums[tmp] == tmp)return tmp;	//看看你家里萝卜是否和你这个一样，一样就说明多了
            else swap(nums[tmp],nums[i]);	//不一样的话交换
        }
    }
    return -1;
}

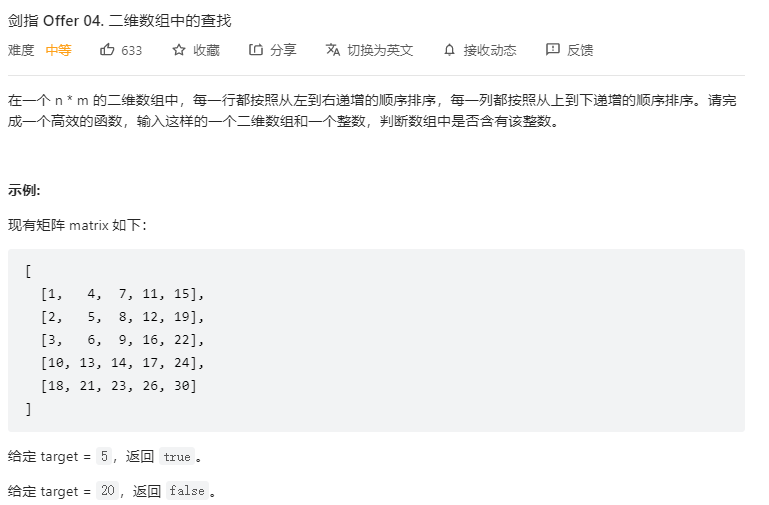
剑指offer04. 二维数组中的查找

image-20220329094331334

这种有规律的题目应该想想如何优化？？？

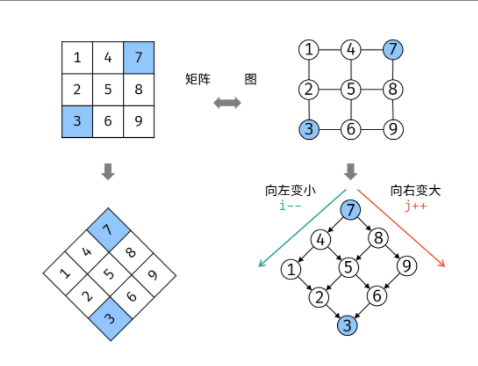
image-20220329094522470

将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

时间复杂度 O(M+N)：其中，N 和 M分别为矩阵行数和列数，此算法最多循环 M+N次。
空间复杂度 O(1) : i, j 指针使用常数大小额外空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        if(m == 0)return false;
        int n = matrix[0].size();
        for(int i = 0,j = n -1;i < m && j >= 0;){
            if(matrix[i][j] == target)return true;
            else if(matrix[i][j] > target)j--;
            else if(matrix[i][j] < target)i++;
        }
        return false;
    }
};

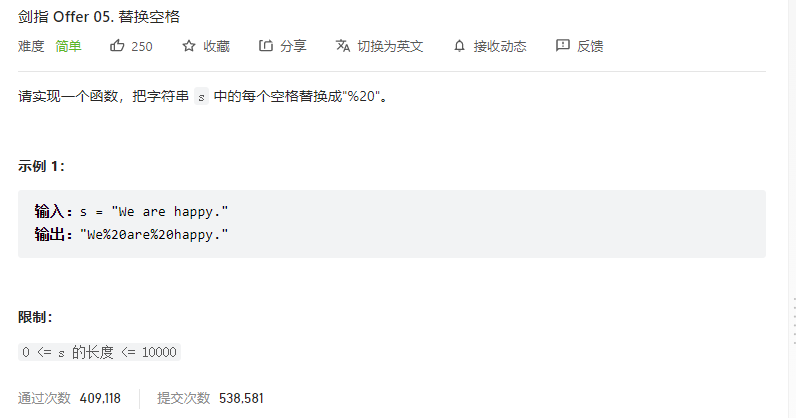
剑指offer05. 替换空格

image-20220329134209325

无脑的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    string replaceSpace(string s) {
        string ans;
        for(auto e : s){
            if(e == ' '){
                ans += "%20";
            }
            else{
                ans += e;
            }
        }
        return ans;
    }
};

不依赖额外空间的方法，先resize()再从后向前双指针操作

其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    string replaceSpace(string s) {
        int size = s.length();
        int oldSize = size;
        for(int i = 0;i < s.length();i++){
            if(s[i] == ' ')size+=2;
        }
        s.resize(size);
        for(int l = oldSize - 1,r = size - 1;l >= 0;l--,r--){
            if(s[l] != ' '){
                s[r] = s[l];
            }
            else {
                s[r] = '0';
                s[r - 1] = '2';
                s[r - 2] = '%';
                r -= 2; 
            }
        }
        return s;
    }
};

剑指 Offer 06. 从尾到头打印链表

image-20220329134637925

递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<int>results;
    vector<int> reversePrint(ListNode* head) {
        helper(head);
        return results;
    }
    void helper(ListNode* head) {
        if(head == nullptr)return;
        helper(head->next);
        results.push_back(head->val);
    }
};

栈：（反向打印竟然想不到栈？？？）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        ListNode* cur = head;
        stack<int>st;
        while(cur != nullptr){
            st.push(cur->val);
            cur = cur->next;
        }
        vector<int>results;
        while(!st.empty()){
            results.push_back(st.top());
            st.pop();
        }
        return results;
    }
};

剑指 Offer 07. 重建二叉树

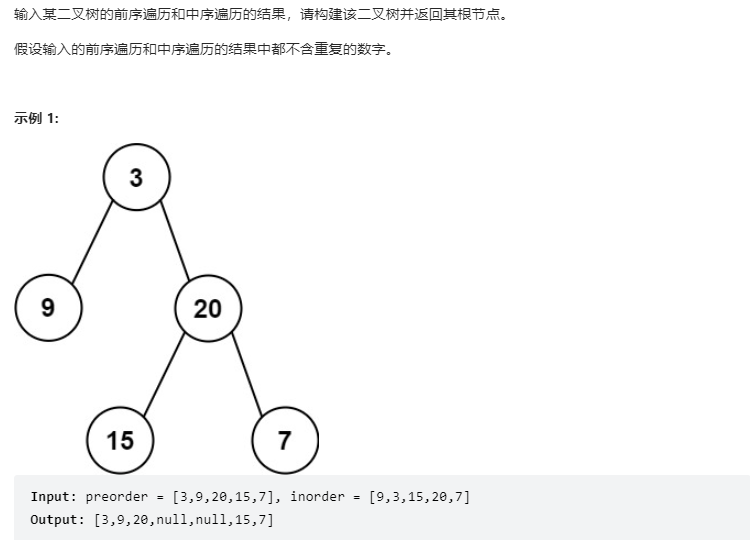
image-20220329135038366

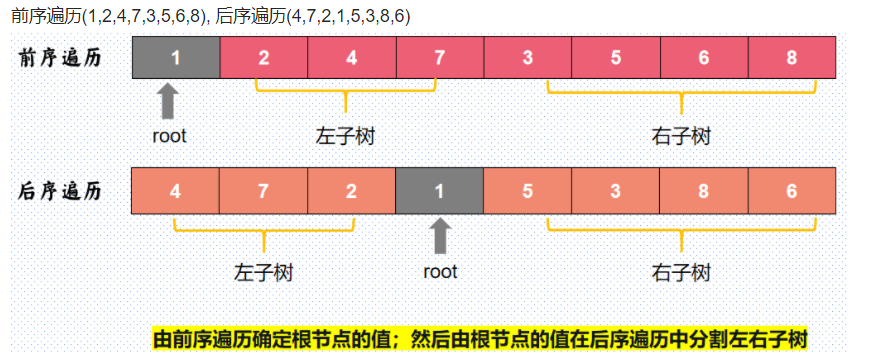
递归的重要思想就是划分为状态相同的子问题

现在我这里有两个序列前序和中序，

image-20220329135507880

因此划分出范围即可，可以增添四个辅助变量分别表示前序范围和后序范围

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildTree(preorder,inorder,0,(int)preorder.size()-1,0,(int)inorder.size()-1);
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder,int l1,int r1,int l2,int r2){
        if(r1 < l1)return nullptr;

        int rt = preorder[l1];
        int len = 0;
        while(inorder[l2+len] != rt)len++;
        TreeNode* root = new TreeNode(preorder[l1]);

        root->left = buildTree(preorder,inorder,l1+1,l1+len,l2,l2+len-1);
        root->right = buildTree(preorder, inorder,l1+len+1,r1,l2+len+1,r2);
        return root;
    }
};

剑指 Offer 09. 用两个栈实现队列

image-20220329135932620

经典题目！！

思路是一个栈看成队尾，一个栈看成队头

  • 然后队尾插入十分简单，仅需stack.push(value)即可
  • 队头取出略有复杂
    1.如果队头不为空，直接取出即可
    2.如果队头为空，将队尾的元素全部倒腾到队头这里，再取出即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class CQueue {

    stack<int>inStack;
    stack<int>outStack;
public:
    CQueue() {

    }

    void appendTail(int value) {
        inStack.push(value);
    }

    int deleteHead() {
        if (inStack.empty() && outStack.empty())return -1;
        else if (!inStack.empty() && outStack.empty()) {
            while (!inStack.empty()) {
                outStack.push(inStack.top());
                inStack.pop();
            }
        }
        int res = outStack.top();
        outStack.pop();
        return res;
    }
};

剑指 Offer 11. 旋转数组的最小数字

image-20220329141428398

这个题注意比较的基准值应当是nums[end]

为什么本题二分法不用 nums[m] 和 nums[i] 作比较？

二分目的是判断 m 在哪个排序数组中，从而缩小区间。而在 nums[m] > nums[begin]情况下，无法判断 m 在哪个排序数组中。本质上是由于nums[end]初始值肯定在右排序数组中； nums[begin]初始值无法确定在哪个排序数组中。

极端情况退化成O(n)
示例一 [1, 0, 1, 1, 1]：旋转点 x = 1 ，因此 m = 2 在 右排序数组 中。
示例二 [1, 1, 1, 0, 1]：旋转点 x = 3，因此 m = 2在 左排序数组 中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minArray(vector<int>& nums) {
        int l = -1, end = nums.size() - 1,r = nums.size();
        while(l + 1 != r){
            int mid = l + (r-l)/2;
            if(nums[mid] > nums[end])l = mid;
            else if(nums[mid] < nums[end])r = mid;
            else{
                int k;
                for(k = 0;k < end;k++){
                    if(nums[k] < nums[end]) break;
                }
                return nums[k];
            }
        }
        return nums[r];
    }
};

剑指 Offer 12. 矩阵中的路径

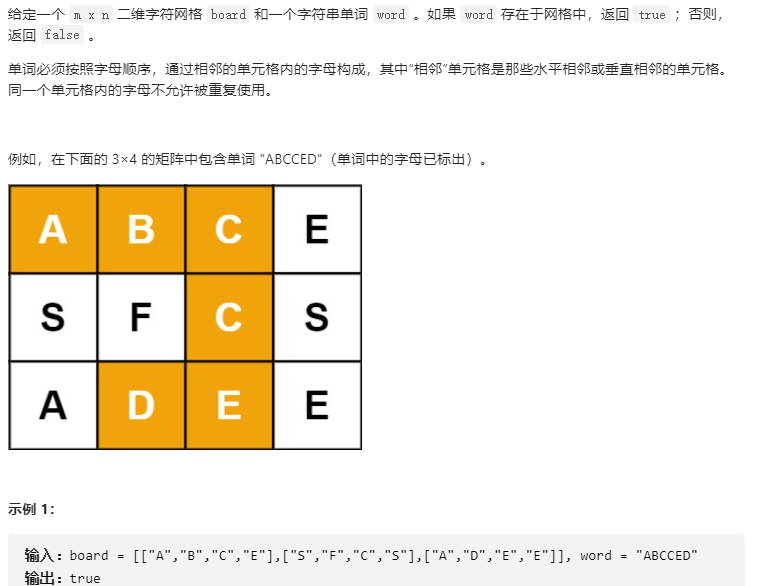
image-20220329142044622

深度优先搜索+回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        
        int m = board.size(),n=board[0].size();
        for(int i = 0;i < m;i++)
            for(int j = 0;j < n;j++)
                if(dfs(board,word,i,j,0))return true;

        return false;
    }

    bool dfs(vector<vector<char>>& board, string word,int m,int n,int i)
    {
        if(i == word.size()-1)return true;
        //剪枝操作
        if(m >= board.size()||n >= board[0].size()||m < 0||n < 0||board[m][n] != word[i])return false;
        char tmp = board[m][n];
        board[m][n] = '\0';
        bool res = dfs(board,word,m+1,n,i+1)||dfs(board,word,m-1,n,i+1)
        ||dfs(board,word,m,n+1,i+1)||dfs(board,word,m,n-1,i+1);
        board[m][n] = word[i];
        return res;
    }
};

剑指 Offer 13. 机器人的运动范围

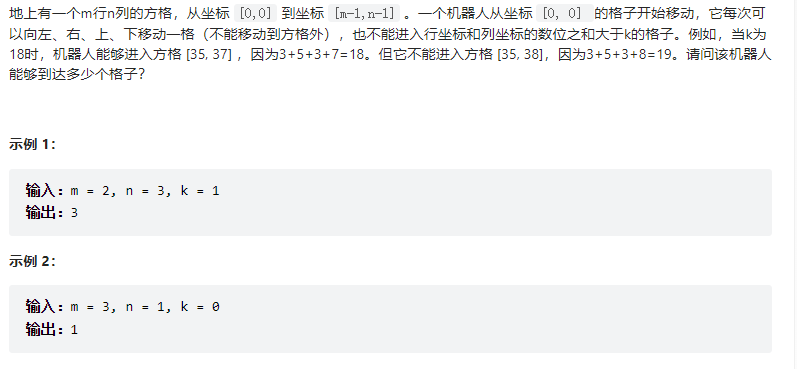
image-20220329143210527

dfs深度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    int res;
    int des[2][2] = {{0,1},{1,0}};
    int m,n;
    int movingCount(int m, int n, int k) {
        this->m = m;this->n = n;
        vector<vector<bool>>visited(m, vector<bool>(n, false));
        res = 0;
        if(k >= 0)dfs(visited, 0, 0, k);
        return res;
    }

    void dfs(vector<vector<bool>>& visited, int i, int j, int maxs)
    {
        visited[i][j] = true;
        res++;
        for(int k = 0;k < 2;k++){
            int tmpi = i + des[k][0];
            int tmpj = j + des[k][1];
            if(tmpi >= m || tmpj >= n || visited[tmpi][tmpj] || !reach(tmpi,tmpj,maxs))continue;
            dfs(visited,tmpi,tmpj,maxs);
        }
    }
    bool reach(int i, int j, int k)
    {
        int m = 0;
        while (i > 0) {
            m += i % 10;
            i /= 10;
        }
        while (j > 0) {
            m += j % 10;
            j /= 10;
        }
        return m <= k;
    }
};

剑指 Offer 29. 顺时针打印矩阵

DFS深度优先遍历

注意这个DFS遍历每个节点应有两种情况
1.下一个节点未被访问，那么直接遍历访问下一个节点（dfs只试了一个方向）
2.下一个节点已经被访问了，那么修改访问方向，继续访问下一个节点（dfs试了两个方向）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<bool>>visited;
    int m,n,d;//m,n表示边界，d表示4个中选取哪一个方向
    int des[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};//四种方向
    vector<int>results;
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        m = matrix.size();
        n = matrix[0].size();
        d = 0;
        visited = vector<vector<bool>>(m,vector<bool>(n,false));
        dfs(matrix,0,0);
        return results;
    }
    void dfs(vector<vector<int>>& matrix,int i,int j){
        if(i < 0 || j < 0 || i >= m || j >= n || visited[i][j]){
            d++;return;
        }
        visited[i][j] = true;
        results.push_back(matrix[i][j]);
        int tmp = d;
        dfs(matrix,i+des[d%4][0],j+des[d%4][1]);
        if(d != tmp)dfs(matrix,i+des[d%4][0],j+des[d%4][1]);//这里发生了偏转
    }
};

这里的方法不需要记录已经走过的路径，所以执行用时和内存消耗都相对较小

  1. 首先设定上下左右边界
  2. 其次向右移动到最右，此时第一行因为已经使用过了，可以将其从图中删去，体现在代码中就是重新定义上边界
  3. 判断若重新定义后，上下边界交错，表明螺旋矩阵遍历结束，跳出循环，返回答案
  4. 若上下边界不交错，则遍历还未结束，接着向下向左向上移动，操作过程与第一，二步同理
  5. 不断循环以上步骤，直到某两条边界交错，跳出循环，返回答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int top = matrix.size() - 1;
        if (top == -1)return vector<int>{};
        int right = matrix[0].size() - 1;
        int left = 0, bottom = 0;
        vector<int>results;

        while (true) {
            for (int i = left; i <= right; i++)results.push_back(matrix[bottom][i]);
            bottom++;
            if (bottom > top)break;

            for (int i = bottom; i <= top; i++)results.push_back(matrix[i][right]);
            right--;
            if (left > right)break;

            for (int i = right; i >= left; i--)results.push_back(matrix[top][i]);
            top--;
            if (bottom > top)break;

            for (int i = top; i >= bottom; i--)results.push_back(matrix[i][left]);
            left++;
            if (left > right)break;
        }
        return results;
    }
};

剑指 Offer 14- I. 剪绳子

image-20220402145248448

方法一：动态规划

dp[i] = max(dp[i],dp[i-j]*dp[j]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int cuttingRope(int n) {
        vector<int>dp(n+1,0);
        if(n == 2)return 1;
        if(n == 3)return 2;
        
        dp[1] = 1;dp[2] = 2;dp[3] = 3;

        for(int i = 4;i <= n;i++){
            for(int j = 1;j < i;j++){
                dp[i] = max(dp[i],dp[i-j]*dp[j]);
            }
        }
        return dp[n];
    }
};

方法二：贪心

有3切3，无3不切

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    //有3切3，无3不切
    int cuttingRope(int n) {
        if(n <= 3){
            return n - 1;
        }
        long long res = 1;
        for(;n > 4;n -= 3)
        {
            res = (3 * res)%1000000007;
        }
        res = (n * res)%1000000007;
        return (int)res;
    }
};

剑指 Offer 15. 二进制中1的个数

image-20220402145900196

初始化数量统计变量 res = 0。

  1. 循环逐位判断： 当 n = 0 时跳出。
  2. res += n&1 ： 若n&1=1 ，则统计数 res 加一。
  3. n >>= 1 ： 将二进制数字 n 无符号右移一位。

返回统计数量 res 。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int sum = 0;
        for(;n > 0;n = (n >> 1) ){
            sum += n&1;
        }
        return sum;
    }
};

剑指 Offer 16. 数值的整数次方

image-20220402150112680

image-20220402150901747

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    double myPow(double x, int m) {
        long n = m;
        if(n < 0){
            x = 1/x;
            n = -n;
        }

        double res = 1;
        while(n > 0){
            if((n & 1) == 1){
                res *= x;
            }
            x *= x;//x x^2 x^
            n = (n >> 1);
        }
        return res;
    }
};

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

image-20220428212958499

剑指 Offer 26. 树的子结构

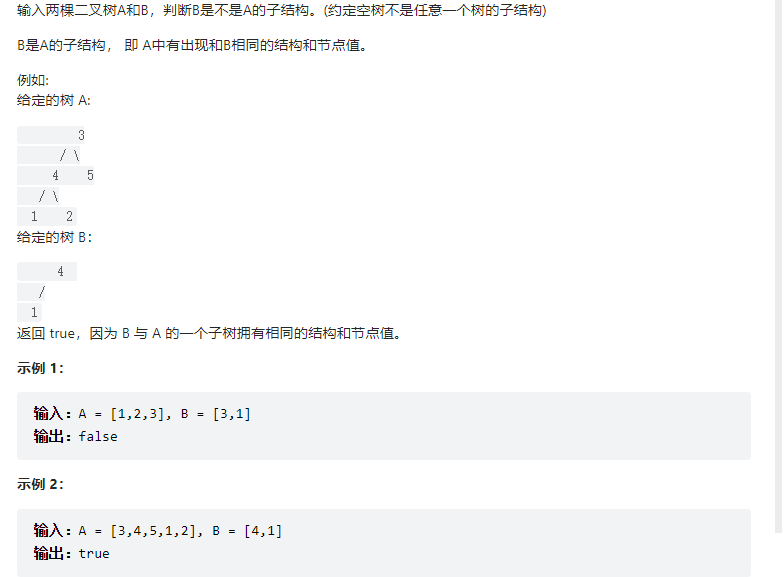
image-20220428221031874

递归先序遍历打印二叉树节点

  1. 先用先序遍历找到A中B的相等节点
  2. 再以这个节点为根节点开始判断两个树结构是否相等
  3. 如果结构不相等再继续寻找下一个相等节点
  4. 把搜索的代码合并到默认的函数里，代码最终可以优化成点赞第一的那个

这个题目必须要加上一个辅助函数用于判断 以此节点为根节点和树B的结构是否相同，因此辅助函数逻辑如下：
如果B已经为空，B这边的结构已经判断完了，可以返回true了
如果A已经为空，但是B那边结构还有节点，这必然无法构成相同结构，返回false
A和B均不为空，那么判断A和B的值是否相等并且递归的判断A和B的左右子树

主功能函数：
思路很简单，先序遍历，如果碰到以当前节点为根节点与树B的结构相同，返回true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    bool compare(TreeNode*A, TreeNode* B){
        if(B == nullptr)return true;
        if(A == nullptr)return false;
        return A->val == B->val&&compare(A->left,B->left)&&compare(A->right, B->right);
    }
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(A == nullptr || B == nullptr ) return false;

        if(compare(A, B))return true;
        return isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
};

剑指 Offer 40. 最小的k个数

方法一：谨记快排是怎么写的，稍作修改即可

方法二：谨记堆排怎么写的

10. 正则表达式匹配

image-20220405160820576

三种情况

  1. s[i] == p[j]最简单的情况dp[i][j] = dp[i-1][j-2];
  2. p[j] == '.'也是非常简单的情况和上面一样dp[i][j] = dp[i-1][j-2];
  3. p[j] == '*'最复杂的情况，又得细分一下：
    如果s[i]!=p[j-1]&&p[j-1]!='.'即p字符串里*前面1位的元素是无法匹配上s的当前元素，那么必然的不应该使用上p字符串这两个字符（#*）dp[i][j] = dp[i][j-2];
    否则* 前面那个字符，能匹配 s[i]，或者 * 前面那个字符是万能的，比如###b和###b*就判断###b和### dp[i][j-2] 以及###b和###b dp[i][j-1]以及###和###b* dp[i-1][j]是否相等

只初始化了dp[0][0]为真，在s和p前面加了2个字符’0’(其他符号也行)，解决了s为空时的特殊情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool isMatch(string s, string p) {
        s = "00"+s;
        p = "00"+p;
        int len1 = s.length(),len2 = p.length();
        vector<vector<bool>>dp(len1,vector<bool>(len2,false));
        dp[0][0] = true;
        for(int i = 1;i < len1;i++){
            for(int j = 1;j < len2;j++){
                if(s[i] == p[j]||p[j] == '.')dp[i][j] = dp[i-1][j-1];
                else if(p[j] != '*')dp[i][j] = false;
                else if(p[j] == '*'){
                    if(s[i]!=p[j-1]&&p[j-1]!='.')dp[i][j] = dp[i][j-2];
                    else {
                        dp[i][j] = dp[i][j-1] || dp[i][j-2] || dp[i-1][j];
                    }
                }
            }
        }
        return dp[len1-1][len2-1];
    }
};

15. 三数之和

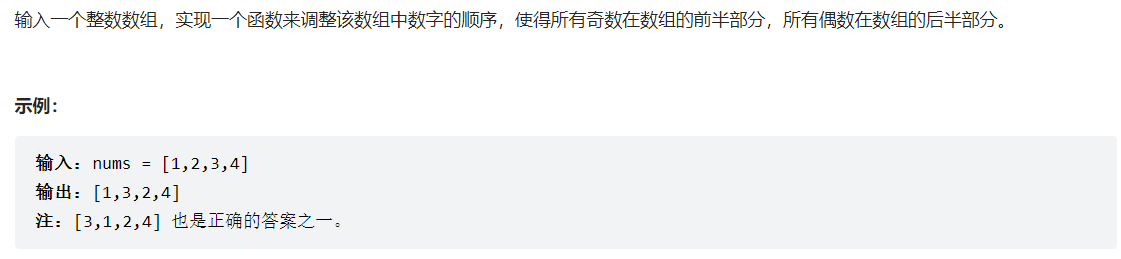
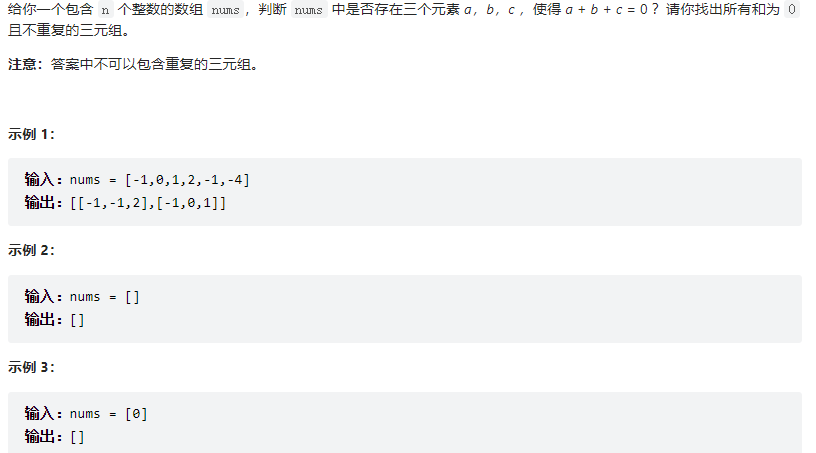
image-20220329164025903

回溯超时不推荐

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>>results;
    vector<int>r;
    vector<bool>visited;
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        visited = vector<bool>(nums.size(),false);
        dfs(nums,0);

        return results;
    }
    void dfs(vector<int>&nums,int start){
        if(r.size() == 3 && r[0] + r[1] + r[2] == 0){
            results.push_back(r);
            return;
        }
        else if(r.size() == 3 ){
            return;
        }
        for(int i = start;i < nums.size();i++){
            if(i > 0 && nums[i] == nums[i - 1] && !visited[i-1])continue;
            visited[i] = true;
            r.push_back(nums[i]);
            dfs(nums,i + 1);
            visited[i] = false;
            r.pop_back();
        }
    }
};

双指针

本质而言，对于排好序的数组，寻找两数之和可以使用双指针，时间复杂度仅为O(n)。

这里只需将第一个数num1的相反数-num1作为target，然后两数之和的双指针解法即可。

另外注意本题不允许重复选取值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<vector<int>>results;
    vector<vector<int>> threeSum(vector<int>& nums) {
        if(nums.size() <= 2)return results;//不足3个数字

        sort(nums.begin(),nums.end());
        for(int i = 0;i < nums.size() - 2;i++){
            if(nums[i] > 0)break;
            if(i > 0 && nums[i] == nums[i-1])continue;//不可重复选
            int l = i + 1;
            int r = nums.size() - 1;
            int target = -nums[i];
            while(l < r){
                if(nums[l] + nums[r] == target){
                    results.push_back(vector<int>{nums[i],nums[l],nums[r]});
                    while(l < r&&nums[l] == nums[l+1])l++;//不可重复选取
                    while(l < r&&nums[r] == nums[r-1])r--;//不可重读选取
                    l++;r--;
                }
                else if(nums[l] + nums[r] > target){
                    r--;
                }
                else if(nums[l] + nums[r] < target){
                    l++;
                }
            }
        }
        return results;
    }
};

11. 盛最多水的容器

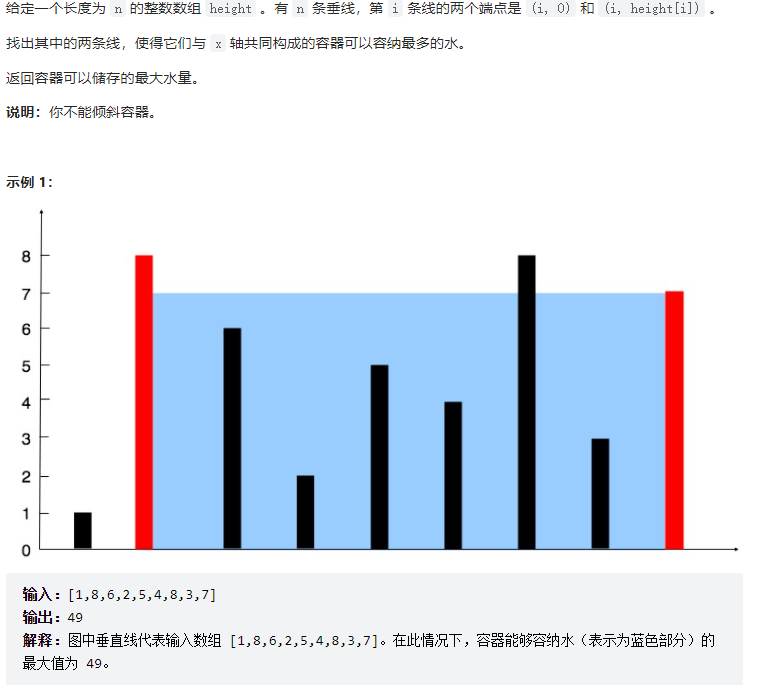
image-20220329175104229

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1 变短：

若向内 移动短板 ，水槽的短板 min(h[i], h[j])可能变大，因此下个水槽的面积 可能增大 。
若向内 移动长板 ，水槽的短板 min(h[i], h[j])不变或变小，因此下个水槽的面积 一定变小 。
因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxArea(vector<int>& height) {
        int maxA = 0;
        int l = 0,r = height.size() - 1;
        while(l < r){
            if(height[l] < height[r]){
                maxA = max(maxA,(r - l)*height[l] );
                l++;
            }
            else {
                maxA = max(maxA,(r - l)*height[r] );
                r--;
            }
        }
        return maxA;
    }
};

31. 下一个排列

image-20220331152049850

标准的“下一个排列”算法可以描述为：

  1. 从后向前查找第一个相邻升序的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
  2. 在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
  3. 将 A[i] 与 A[k] 交换
  4. 可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
  5. 如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int size = nums.size();
        int left;
        for (left = size - 2; left >= 0; left--) {
            if (nums[left] < nums[left + 1])break;
        }
        if (left == -1)return reverse(nums.begin(), nums.end());

        int right;
        for (right = size - 1; right > left; right--) {
            if (nums[right] > nums[left])break;
        }
        swap(nums[right], nums[left]);
        reverse(nums.begin() + left + 1, nums.end());
        return;
    }
};

32. 最长有效括号

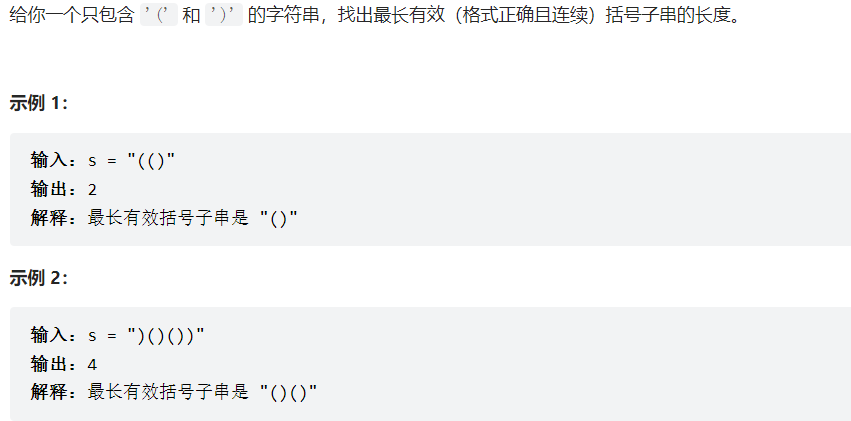
image-20220405172637504

  • 先用栈把左括号记录起来
  • 开个数组记录那些括号已经匹配
  • 遇到右括号就把右括号和遇到的左括号记录
  • 最后遍历一遍记录数组即可
  • 时间:O(n) 空间:O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int>st;
        int len = s.length();
        vector<bool>sv(len,false);
        for(int i = 0;i < len;i++){
            if(s[i] == '(')st.push(i);
            else if(s[i] == ')'){
                if(!st.empty()){
                    sv[i] = true;
                    sv[st.top()] = true;
                    st.pop();
                }
            }
        }

        int maxl = 0;
        int continuous = 0;
        for(int i = 0;i < len;i++){
            if(sv[i] == true)continuous++;
            else continuous = 0;
            maxl = max(maxl,continuous);
        }
        return maxl;
    }
};

98. 验证二叉搜索树

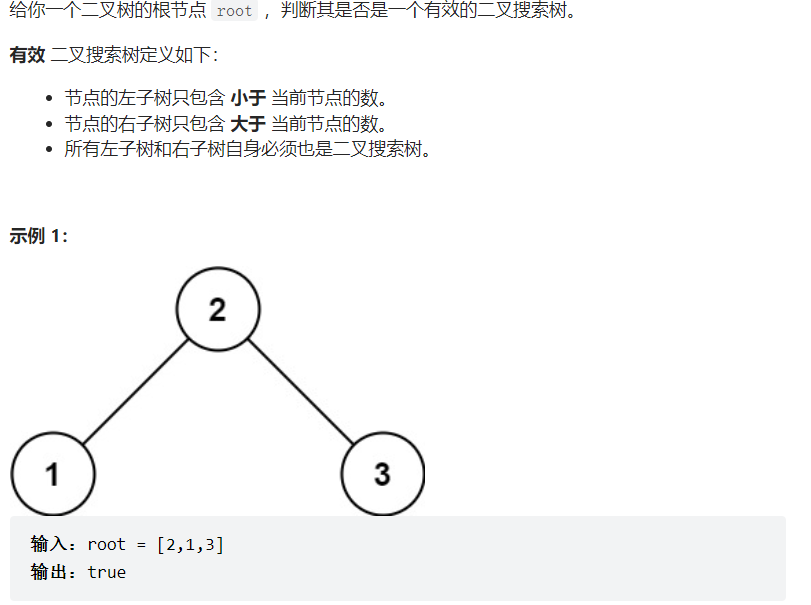
image-20220405175210665

方法一：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return isValidBST(root,-2147483649,2147483648);
    }
    bool isValidBST(TreeNode* root,long long minn,long long maxn){
        if(root == nullptr)return true;
        bool ret = root->val < maxn && root->val > minn;
        ret = ret && isValidBST(root->left,minn,root->val) 
            && isValidBST(root->right,root->val,maxn);
        return ret;
    }
};

方法二：中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    long long pre = LONG_MIN;
    bool ret = true;
    bool isValidBST(TreeNode* root) {
        preorder(root);
        return ret;
    }
    void preorder(TreeNode* root){
        if(root == nullptr)return;
        preorder(root->left);
        if(pre >= root->val){//大于前面的肯定得返回false
            ret = false;
            return;
        }
        else pre = root->val;//更新pre
        preorder(root->right);
    }
};

注意要使用longlong，因为测试用例包含了INT_MIN

48. 旋转矩阵

image-20220403170835769

官方题解写的很好

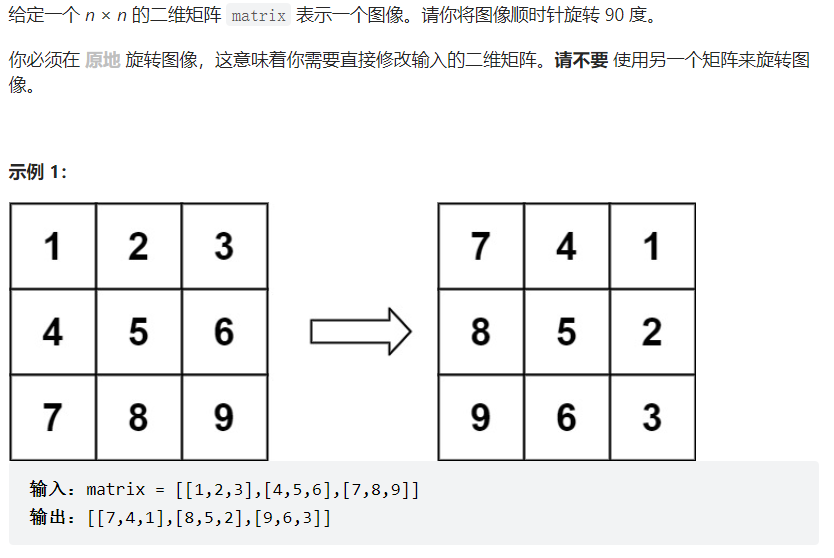
方法一：

借助临时变量，一个一个翻转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};

方法二：

先上下翻转矩阵，再沿对角线翻转矩阵，简单粗暴且不犯错

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int len = matrix.size();
        for(int i = 0,j = len - 1;i < j;i++,j--){
            for(int k = 0;k < len;k++){
                swap(matrix[i][k],matrix[j][k]);
            }
        }
        for(int i = 0;i < len;i++){
            for(int k = i + 1;k < len;k++){
                swap(matrix[i][k],matrix[k][i]);
            }
        }
    }
};

75. 颜色分类

image-20220404165928303

0，1，2 排序。一次遍历，如果是0，则移动到表头，如果是2，则移动到表尾，不用考虑1。0和2处理完，1还会有错吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    void sortColors(vector<int>& nums) {
        int len = nums.size();
        if(len < 2)return;  
        int two = len - 1;
        int zero = 0;
        int i = 0;
        while(i <= two){
            if(nums[i] == 0){
                swap(nums[zero],nums[i]);
                zero++;
                i++;
            }
            else if(nums[i] == 1){
                i++;
            }
            else if(nums[i] == 2){
                swap(nums[two],nums[i]);
                two--;
            }
        }
    }
};

253. 会议室 II

image-20220415110954685

题目就是要统计同一时刻进行的最大会议的数量
我们可以把所有的开始时间和结束时间放在一起排序，
用cur表示当前进行的会议数量，遍历排序后的时间数组
如果是开始时间，cur加1，如果是结束时间，cur减一
在遍历的过程中，cur出现的最大值就是需要的房间数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    static bool cmp(vector<int>&a,vector<int>&b){
        if(a[0] == b[0])return a[1] < b[1];
        return a[0] < b[0];
    }
    int minMeetingRooms(vector<vector<int>>& intervals) {
        vector<vector<int>>time;
        for(auto &t : intervals){
            time.push_back(vector<int>{t[0],1});
            time.push_back(vector<int>{t[1],-1});
        }
        sort(time.begin(),time.end(),cmp);

        int cur = 0;
        int maxi = 0;
        for(auto&t : time){
            if(t[1] == 1)cur++;
            else cur--;
            maxi = max(cur,maxi);
        }
        return maxi;
    }
};

283. 移动零

image-20220415112150483

方法一：双指针，每当出现0的时候，左指针回退一格即可（因为第一次遍历的时候0无需存储）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int left = 0;
        int right = 0;
        for(;right < nums.size();right++,left++){
            nums[left] = nums[right];
            if(nums[right] == 0){
                left--;
            }
        }
        for(;left < nums.size();left++){
            nums[left] = 0;
        }
    }
};

581. 最短无序连续子数组

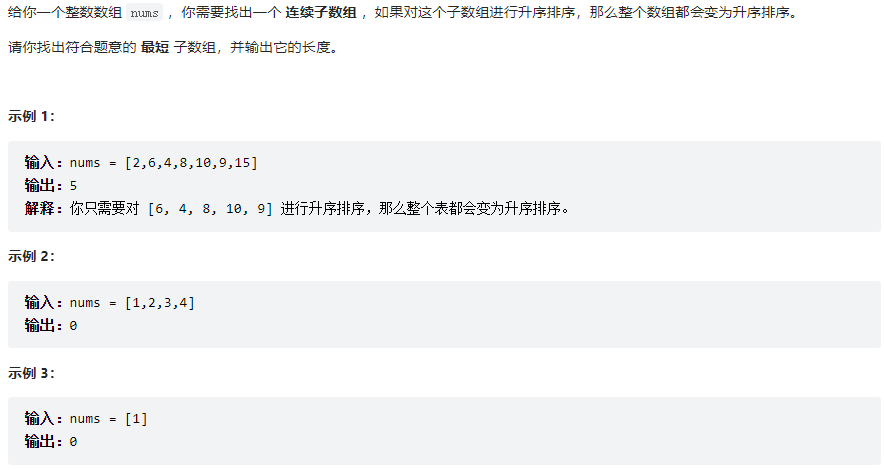
image-20220422101231673

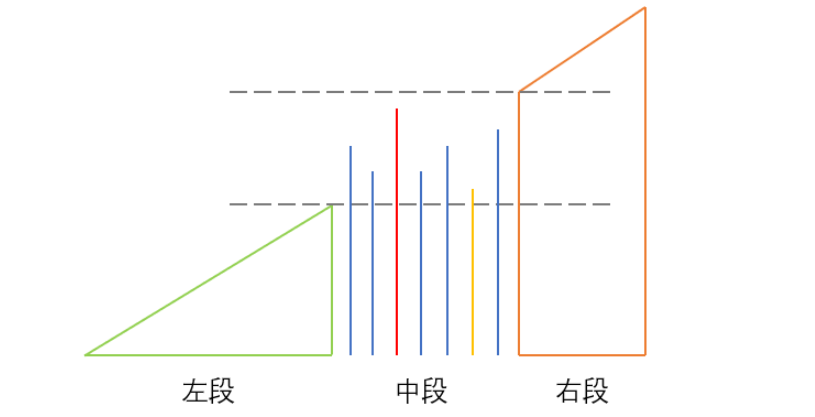
我们可以假设把这个数组分成三段，左段和右段是标准的升序数组，中段数组虽是无序的，但满足最小值大于左段的最大值，最大值小于右段的最小值。

image-20220422101531995

那么我们目标就很明确了，找中段的左右边界，我们分别定义为begin 和 end;
分两头开始遍历:

  • 从左到右维护一个最大值max,在进入右段之前，那么遍历到的nums[i]都是小于max的，我们要求的right就是遍历中最后一个小于max元素的位置；
  • 同理，从右到左维护一个最小值min，在进入左段之前，那么遍历到的nums[i]也都是大于min的，要求的left也就是最后一个大于min元素的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int maxn = INT_MIN;int minn = INT_MAX;
        int left = -1;int right = -1;
        int len = nums.size();

        //寻找right
        for(int i = 0;i < len;i++){
            if(nums[i] >= maxn) maxn = nums[i];
            else right = i;//出现无序情况，更新right
        }
        //寻找left
        for(int i = len - 1;i >= 0;i--){
            if(nums[i] <= minn) minn = nums[i];
            else left = i;//出现无序情况，更新left
        }

        return right == -1 ? 0 : right - left + 1;
    }
};

621. 任务调度器

image-20220422104700429

任务调度器C++ 桶子_配图理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int len = tasks.size();
        
        vector<int>vec(26,0);
        for(auto task : tasks)vec[task - 'A']++;

        int maxv = 0;
        for(int i = 0;i < 26;i++)maxv = max(maxv,vec[i]);
        
        int cnt = 0;
        for(int i = 0;i < 26;i++){
            if(vec[i] == maxv)cnt++;
        }

        return max(len,(n+1)*(maxv-1) + cnt);
    }
};