求取两数平均值

1
2
3
4
5
6
int a;
int b;
int c = (a+b)/2;
int d = a/2 + b/2;
int e = a/2 + b/2 + 1;
int f = a/2 + b/2 + (a&b&1);

一般情况下(a+b)/2没问题，但是a和b值都过大时会造成溢出！

而a/2 + b/2又有可能产生精度丢失，比如a和b的值都为3，结果是2，少了1 。

那么什么时候需要弥补精度呢？答案是a和b都是奇数，也即a和b的最低位是1

因此最终结果int f = a/2 + b/2 + (a&b&1);既避免精度损失又避免溢出。

求取n个数的平均值

a1,a2,a3,…,an的平均值

如果a1/n+a2/n+a3/n+...+an/n显然有精度损失，那么如何将损失补回去？

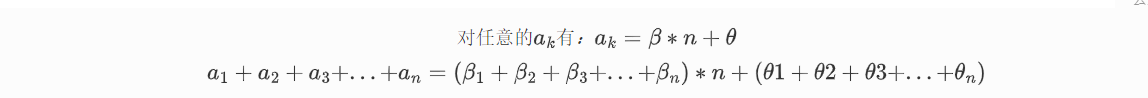
image-20220311094831498

因此思路变为了对于前面能整除部分直接整除再相加，对于后面余数部分将所有余数加起来再除以n即可。

我们可以

1
2
3
4
5
6
7
8
9
10
int average(int a[], int n) {
    int ret = 0;
    int m = 0;
    for (int i = 0; i < n; i++) {
        ret += a[i] / n;
        m += a[i] % n;
    }

    return ret + m/n;
}

但是这样仍然会造成溢出，有两个限制，要求

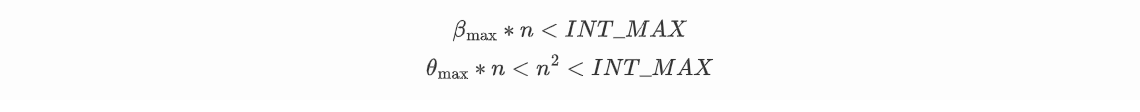
image-20220311094907648

可以继续小小修改一下避免第二个限制，第一个限制仍然无法避免

1
2
3
4
5
6
7
8
9
10
11
int average(int a[], int n) {
    int ret = 0;
    int m = 0;
    for (int i = 0; i < n; i++) {
        ret += a[i] / n;
        m += a[i] % n;
        ret += m / n;
        m = m % n;
    }
    return ret;
}