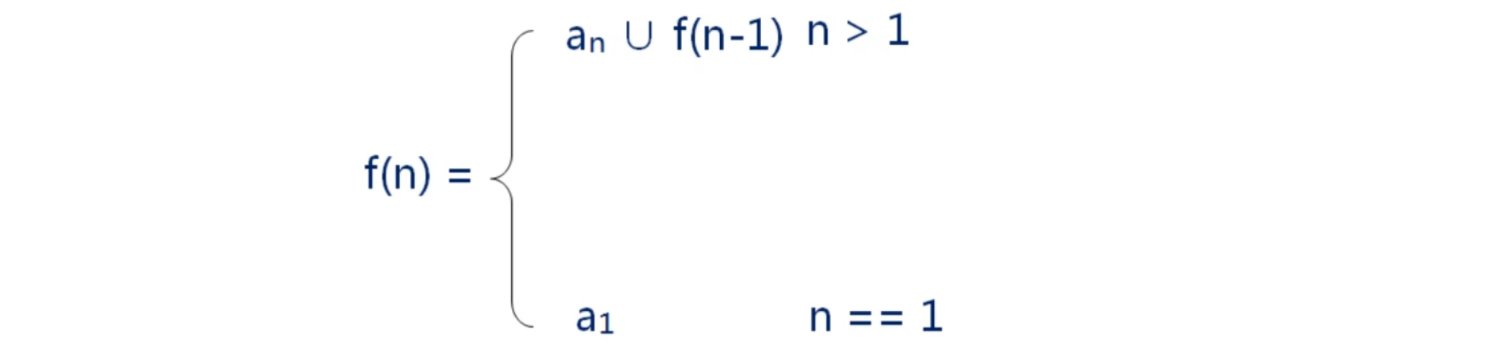什么是递归？

– 递归是一种数学上分而自治的思想（问题分解）
• 分解后的问题与原问题的类型完全相同， 但问题复杂度降低
• 通过相对简单问题（子问题）的解，能够轻易求得原问题的解

– 递归与递推的思想相同，但是表现形式不同
• 递归强调“归”，即：求解子问题后“回到原处”解决当前问题
• 递推强调“逐渐接近”，即：在既定策略下一步一步求解问题

image-20220304163940241

递归在程序设计中的应用
– 递归函数
• 函数体中存在自我调用的函数
• 递归函数必须有递归出口（边界条件）
• 函数的无限递归将导致程序崩溃（函数调用栈越界）

递归与递推本质差异
– 递归在求解原问题时：
• 可能将原问题分解为多个子问题，并等待所有子问题求解结束
• 得到所有子问题答案后，需要对子问题答案进行汇总，平衡，取舍。。。
– 递推在求解原问题时：
• 假设在既定策略下，能够逐步接近问题答案
• 递推中的策略保证每一个求解步骤总是能接近问题答案

思路：

  1. 先想代码出口，最简单的情况即一眼就能看出结果的情况（例如数组大小为1，树的节点只有1个等等）
  2. 再思考原问题如何分解小问题，找出递归式，注意小问题和原问题的状态应该是一样的
  3. 有时候可能有功能参数，比如记录路径，那么功能参数我们可以设为全局变量或者作为递归函数的引用参数

递归的划分子问题思想

查找一个无序数组的最大值空间复杂度O(log n)

初始思路：

1
2
3
4
5
int MaxInArray(int a[], int n)
{
    if (n == 1)return a[0];
    return std::max(MaxInArray(a, n - 1), a[n - 1]);
}

非常的简单粗暴，但是这样的空间复杂度是O(n)。函数调用栈过深，如果用二分的方式，函数两边的栈的深度差不多，但是总体栈深度大大降低，栈的深度变为了O(log n)

我们应该分而治之的思想，另外注意一般数组递归函数最好要有三个参数（数组自身，begin，end）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int MaxInArray(int a[], int begin, int end)
{
    if (begin == end)return a[begin];
    int mid = begin + ((end - begin) >> 1);

    int lmax = MaxInArray(a, begin, mid);
    int rmax = MaxInArray(a, mid + 1, end);

    return lmax > rmax ? lmax : rmax;
}
int MaxInArray(int a[], int n)
{
    return MaxInArray(a, 0, n - 1);
}

二分子问题可以大大地减少栈深度

但是你以为这就完了吗？不，还有尾递归！

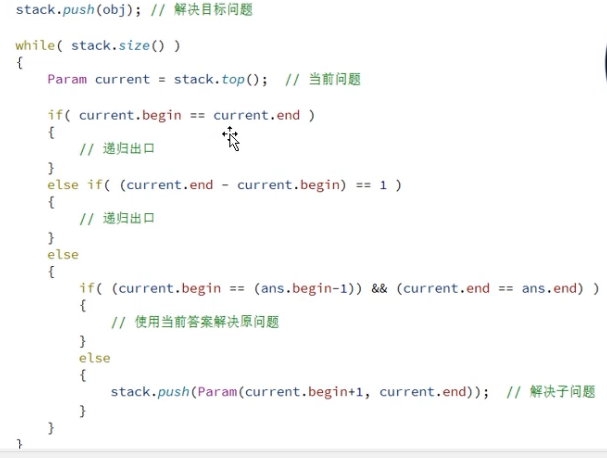
尾递归

递归改为循环

递归到非递归

• 核心：抓住递归的本质， 使用栈数据结构模拟递归调用
入栈操作：尝试解决问题
出栈操作：得到问题答案

可使用栈数据结构模拟递归过程：

  1. 当前问题参数入栈（递归调用）
  2. 参数出栈时，使用当前答案解决问题
  3. 标记当前问题已解决

注意 递归思想的非递归描述

  1. 只是模拟递归调用的过程
  2. 在代码结构上与递归实现几乎相同
    • 存在递归出口（直接得到答案）
    • 存在利用子问题答案求解原文题的代码片段

框架：

image-20220324102520227

求取集合的子集

尝试编写一个递归函数，用来输出 n 个元素的所有子集
• 例如：集合 { a, b, c } 的所有子集是：
{ }， { a }， { b }， { c }， { a, b }， { b, c }， { a, c }， { a, b, c }
思维起点
• 如何表示一个集合？递归函数的参数和返回值如何定义？
• 如何分解出子问题？如何利用子问题的答案解出当前问题？

这个题目表面上很简单，但并不是的！

1

删除无序链表重复节点

已知无序链表 L ，编写递归函数删除链表中的重复结点
示例： 1->3->1->5->3->5->7，删除重复结点后 1->3->5->7
要求：未被删除的结点，相对次序不能改变 

1

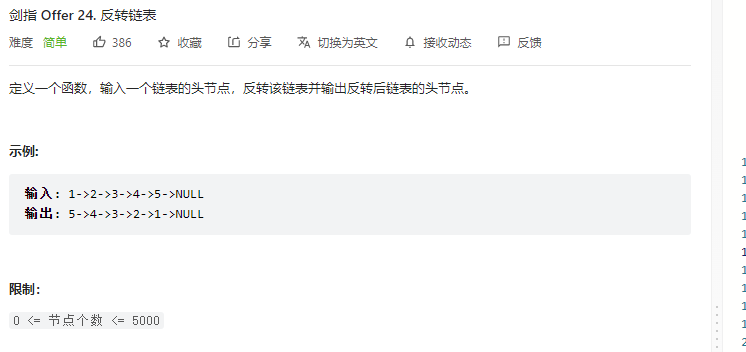
反转链表（简单）

image-20220304164838880

1
2
3
4
5
6
7
8
9
ListNode* reverseList(ListNode* head) {
    if (!head || !head->next) {
        return head;
    }
    ListNode* newHead = reverseList(head->next);
    head->next->next = head;
    head->next = nullptr;
    return newHead;
}

二叉树和为某一值的路径

image-20220304165022265

思维起点
– 二叉树是递归定义的， 所以首选递归解法
– 考虑简单情况：
• 当二叉树只有根结点：直接比较
• 当二叉树有多个结点：
在左子树中查找是否存在和为 (x - vroot) 的路径
在右子树中查找是否存在和为 (x - vroot) 的路径 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>>res;
    vector<int>path;
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        dfs(root,target);
        return res;
    }
    void dfs(TreeNode* root,int target){
        if(root == nullptr)return;

        path.push_back(root->val);

        if(root->left==nullptr&&root->right==nullptr&&root->val == target){
                res.push_back(path); 
        }
        
        if(root->left!=nullptr)dfs(root->left,target-root->val);
        if(root->right!=nullptr)dfs(root->right,target-root->val);
        path.pop_back();
    }

};

特别注意：这一题要判断路径，我们因此必须将路径用容器存储。并且每次遍历了一个节点就将节点存入容器，遍历结束后就将节点pop出。

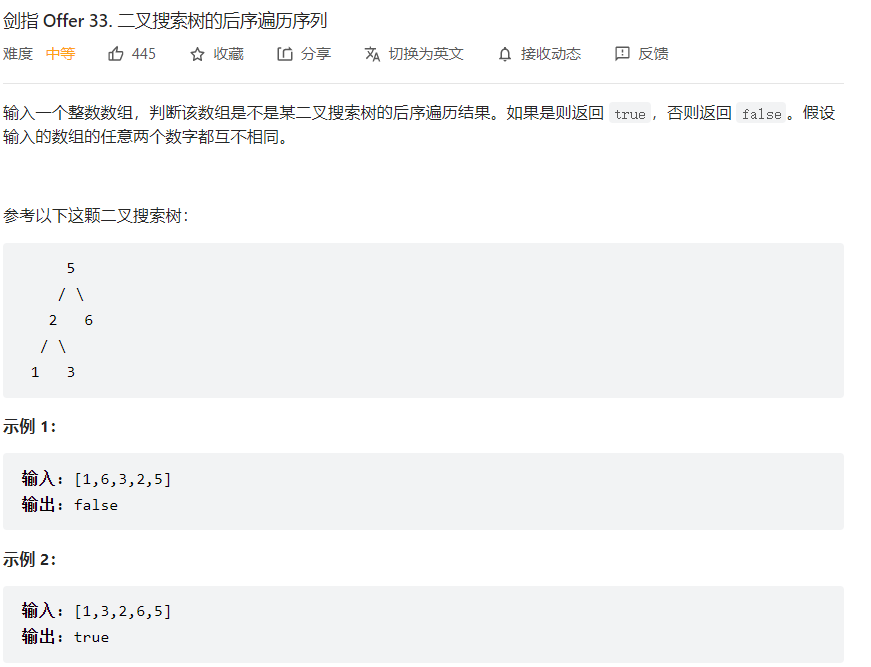
二叉搜索树的后序遍历序列

image-20220304192706113

这个题的关键在于要先将左右子树划分好，划分完了在看左分区的大小是否小于根节点，右分区的大小是否都大于根节点。然后再对左右子树递归判断即可。理清了二叉搜索树的判断那么代码就呼之欲出了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:  
    bool verifyPostorder(vector<int>& postorder) {
        return verifyPostorder(postorder,0,postorder.size() - 1);
    }
    bool verifyPostorder(vector<int>& postorder,int begin,int end) {
        if(end - begin <= 1)return true;
        int mid = begin;
        for(;(mid < end)&&(postorder[mid] < postorder[end]);mid++);        

        for(int i = mid+1;i<end;i++)
            if(postorder[i] < postorder[end])return false;

        return  verifyPostorder(postorder,begin,mid-1) && verifyPostorder(postorder,mid,end-1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
private:
    unordered_map<int, int> index;

public:
    TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return nullptr;
        }
        
        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = index[preorder[preorder_root]];
        
        // 先把根节点建立出来
        TreeNode* root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        // 构造哈希映射，帮助我们快速定位根节点
        for (int i = 0; i < n; ++i) {
            index[inorder[i]] = i;
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
};

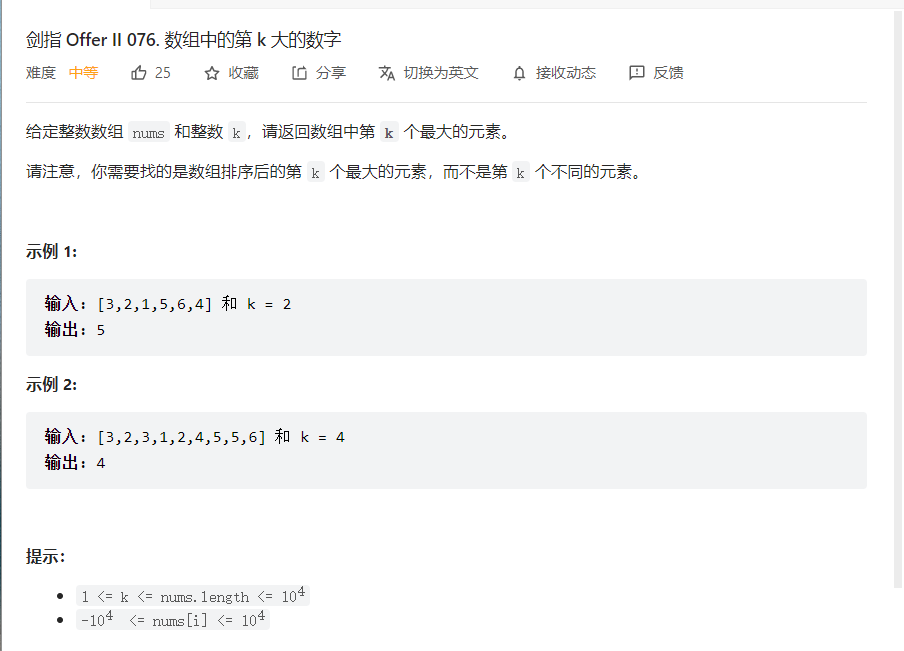
数组中第k大的数字（求取数组的中位数也是此解法）

image-20220312173302799

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int partition(vector<int>& nums, int begin, int end){
        int pivot = nums[begin];
        while(begin < end){
            while(nums[end]<pivot&&begin < end)end--;
            nums[begin] = nums[end];
            while(nums[begin]>=pivot&&begin < end)begin++;
            nums[end] = nums[begin]; 
        }
        nums[begin] = pivot;
        return begin;
    }
    int findKthLargest(vector<int>& nums, int k, int begin, int end) {
        if(begin == end)return nums[begin];
        
        int ret = 0;
        int i = partition(nums, begin, end);
        if(i == k)ret = nums[i]; 
        else if(i > k)ret = findKthLargest(nums, k,begin,i-1);
        else if(i < k)ret = findKthLargest(nums, k,i+1,end);
        return ret;
    }

    int findKthLargest(vector<int>& nums, int k) {
        return findKthLargest(nums, k-1, 0, nums.size() - 1);
    }
};