highlight: vs2015
theme: juejin
红黑树的五个性质:
- 每个结点是红的或者黑的
- 根结点是黑的
- 每个叶子结点是黑的
- 如果一个结点是红的,则它的两个儿子都是黑的
- 对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点
平衡的定义是说从空链接到根节点距离相等,此处一定要用心理解。(也就是说非叶子节点是不会存在空链接的
节点定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #define RED 1
#define BLACK 2
typedef int KEY_TYPE;
typedef struct _rbtree_node {
//红红黑树性质
unsigned char color;
struct _rbtree_node* right;
struct _rbtree_node* left;
struct _rbtree_node* parent;
KEY_TYPE key;
//value
void* value;
} rbtree_node;
typedef struct _rbtree {
rbtree_node* root;
rbtree_node* nil;//哨兵节点
//所有叶子节点都隐藏,并且都设置为黑色
//空节点无颜色,叶子节点有颜色
} rbtree;
|
rbtree_node* nil;//哨兵节点 因为红黑树的所有叶子节点都隐藏,并且都设置为黑色,因此可以用一个nil统一代表所有的叶子节点 nil节点与NULL不能等同,NULL没有颜色,但是nil节点有颜色
左旋和右旋
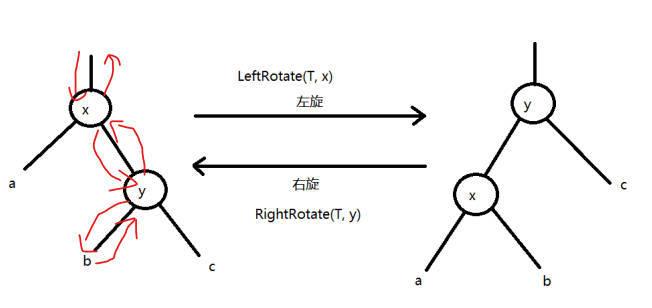
左旋rotate 涉及到三个方向,六个指针的改变,
- 先将x与b相互指向对方
- 再将x的父亲节点与y节点相互指向对方
- 再将x与y的方向修改
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //左旋是以当前节点自己进行下沉
void rbtree_left_rotate(rbtree* T, rbtree_node* x) {
if (x == T->nil)return;
rbtree_node* y = x->right;//y节点
//1 x--b
x->right = y->left;
if (y->left != T->nil) {
y->left->parent = x;
}
//2 x.parent--y
y->parent = x->parent;
if (x->parent == T->nil) {//x为根节点
T->root = y;
}
else if (x == x->parent->left) {
x->parent->left = y;
}
else {
x->parent->right = y;
}
//3 x--y
y->left = x;
x->parent = y;
}
|
右旋的代码仅需将上述的x改为y,y改为x即可实现
插入节点
在插入节点以前就是一棵红黑树,插入一个节点是红的更容易满足红黑树的性质,插入后当前节点是红色的,父节点也是红色的,只可能违背性质4(如果一个结点是红的,则它的两个儿子都是黑的 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil) {
y = x;
if (z->key < x->key) {
x = x->left;
} else if (z->key > x->key) {
x = x->right;
} else { //Exist
return ;
}
}
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
z->color = RED;
rbtree_insert_fixup(T, z);
}
|
先是一个while循环找到应该插入的位置,while循环结束x必定为nil节点,因此借助一个临时变量y节点存储插入节点的父节点,找到位置后依据大小将要插入的z节点插入的适当位置,并且将z置为red。再对上述操作进行颜色的修正,而修正函数在如下给出。
插入修正函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
while (z->parent->color == RED) { //z ---> RED
if (z->parent == z->parent->parent->left) {
rbtree_node *y = z->parent->parent->right;//叔结点
if (y->color == RED) {//叔结点是红色的
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->right) {
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);
}
}else {
rbtree_node *y = z->parent->parent->left;
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
|
这个过程是一个迭代过程,是自下而上的层层调整,因此需要一个while循环,不论什么时候z节点始终扣住自下而上的那条遍历线路,颜色始终是红色的,z节点调整完之后会变为上层的节点直到根节点也调整完为止
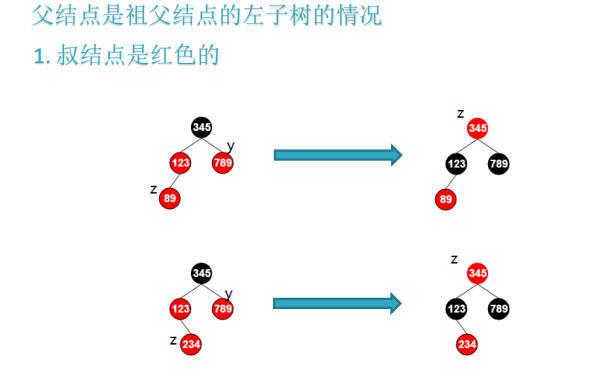
1
2
3
4
5
6
7
| rbtree_node *y = z->parent->parent->right;//叔结点
if (y->color == RED) {//叔结点是红色的
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
}
|
z = z->parent->parent;这是迭代的关键语句
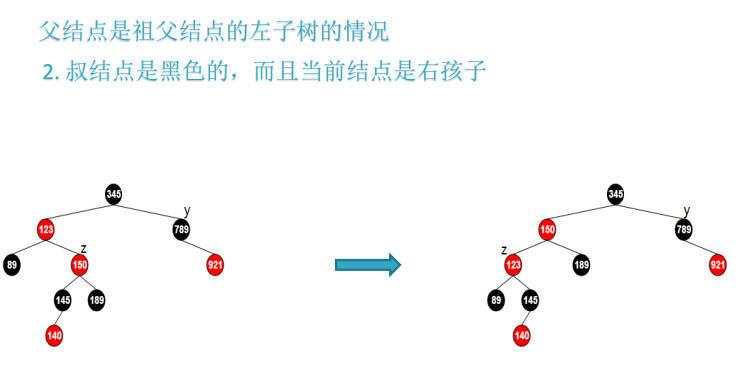
观察第一幅图,叔父y节点的黑高是2,与其他线的黑高不匹配,因此先对z的父节点123进行左旋变为右侧第二幅图,
1
2
3
4
| if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
|
但是这个时候树高度不平衡了,因此要继续修正,先将z父节点置为黑色,z祖父节点置为红色,在对z的祖父节点右旋即可达到平衡
1
2
3
| z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
|
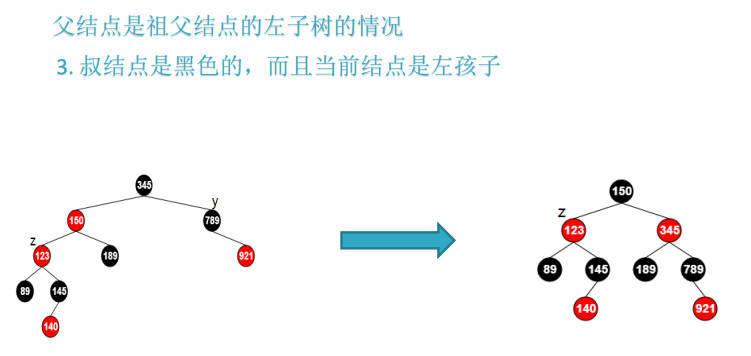
以上就是需要修正的3种情况
删除节点
将结点 z 从二叉查找树 T 中删除共有如下三种情况,其中一种有一点难懂。
- 如果结点 z 没有孩子结点,我们就可以直接使用
NIL 来代替该结点。
- 如果结点 z 只有一个子女,可以直接用结点 z 的孩子结点替代 z 。
- 如果结点 z 有两个子女,首先要找到结点 z 的后继 y (它一定在 z 的右子树中),并用 y 替代 z 在树中的位置。
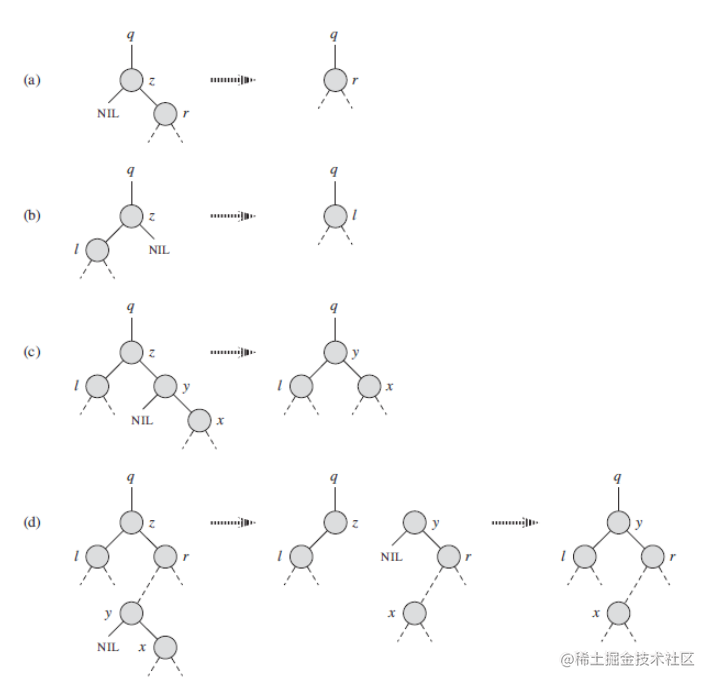
TREE-DELETE 过程用于从二叉查找树 T 中删除一个给定的结点 z ,它按如下四种情况组织代码。
如果结点 z 没有左孩子,那么我们用右孩子替换 z ,其中右孩子可能为 NIL 。右孩子为 NIL 即结点 z 没有孩子结点的情况。(图a)
如果结点 z 有且只有左孩子,那么就用左孩子替代结点 z 。(图b)
否则,结点 z 有两个子结点。首先找到 z 的后继结点 y ,它位于 z 的右子树且没有左孩子。这里我们打算用 y 替换 z 。
- 如果 y 是 z 的右孩子,那么直接用 y 替换 z 。(图C)
- 否则,用 y 自己的右孩子替换 y ,再用 y 来替换 z 。(图d)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| 1. rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {
2.
3. rbtree_node *y = T->nil;
4. rbtree_node *x = T->nil;
5.
6. if ((z->left == T->nil) || (z->right == T->nil)) {
7. y = z;
8. } else {
9. y = rbtree_successor(T, z);
10. }
11.
12. if (y->left != T->nil) {
13. x = y->left;
14. } else if (y->right != T->nil) {
15. x = y->right;
16. } else {
17. x = T->nil;
18. }
19.
20. x->parent = y->parent;
21. if (y->parent == T->nil) {
22. T->root = x;
23. } else if (y == y->parent->left) {
24. y->parent->left = x;
25. } else {
26. y->parent->right = x;
27. }
28.
29. if (y != z) {
30. z->key = y->key;
31. z->value = y->value;
32. }
33.
34. if (y->color == BLACK) {
35. rbtree_delete_fixup(T, x);
36. }
37.
38. return y;
39. }
|

- 这个代码并不是完全按照算法导论上写的,进行了一些优化
- 6-10行一个if-else判断直接将四幅图的y都给确定,图a,b中将z赋值给了y。
- 12-18行的if-else判断直接将四幅图的x都给确定,否则x置为nil,
- 20-27对应transplant操作,将x与y.parent连接起来了
- 29-32对应图c,d的情况,将z与x连接后再将y的值赋给z。
删除修正函数
红黑树的五个性质:
- 每个结点是红的或者黑的
- 根结点是黑的
- 每个叶子结点是黑的
- 如果一个结点是红的,则它的两个儿子都是黑的
- 对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点
我们在每次删除前,对于上面前两幅图中的情况,我们会记录下被删除结点z的颜色,因为它决定了我们最后是否需要修正红黑性质(若z为红色,其父结点和孩子必为黑色,删除z将不会违背性质5,用z的孩子去替代z也不会影响性质4),y指向z,x指向z的右孩子;对于后两种情况,我们记录的是被删除结点z右子树中关键字最小的结点y的颜色,同样,如果它是红色,不管z是什么颜色,统一将y的颜色修改为z的颜色,并按照图中的方式去置换掉z,都不会对红黑性质产生影响。综合上述分析,我们发现四种情况的“输出”(处理后的结果)是一致的:若记录的颜色是红色,说明红黑性质未改变,无需修正;如果是黑色,说明红黑性质一定被打破了,需要修正调用fixup函数。
如果结点y是黑色,如下图,将会造成3种影响:
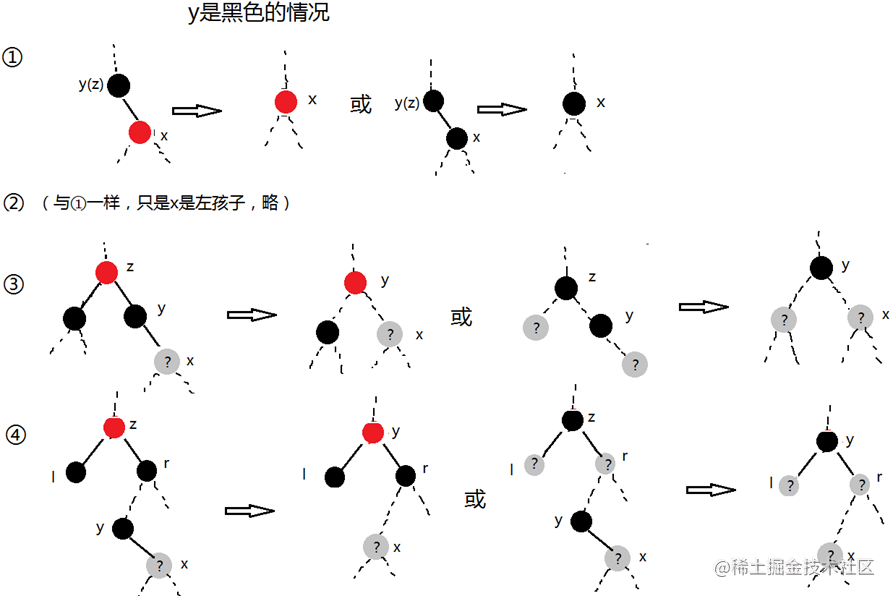
1)如果y原来是根结点,而y的一个红孩子成为了新的根结点,将会违背性质2根结点是黑的。如上图①中左侧情况。
2)如果x和x的父结点都为红色,将违背性质4如果一个结点是红的,则它的两个儿子都是黑的。如上图③中的左侧,x为红色的情况。
3)所有的情况(除了y原来是根结点外)都将导致之前包含y结点的简单路径上的黑结点数少1,将违背性质5对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点。修正这一问题的方式是我们将现在占据y结点位置的x结点“再涂上一层黑色”,当然,“涂色”操作并不反映在代码上,即我们不会修改x的color属性,我们只是“在心中记住”,适当的时候会把x的这层黑色涂到某个红色结点上以达到目的。“涂了两层色”的x结点可能是双层黑色或红黑色,它们分别会“贡献”2或1个黑色结点数。
下面我们再分析RB-DELETE-FIXUP修正过程:
修正过程分了4种情况,我们先给出每种情况对应的示意图:
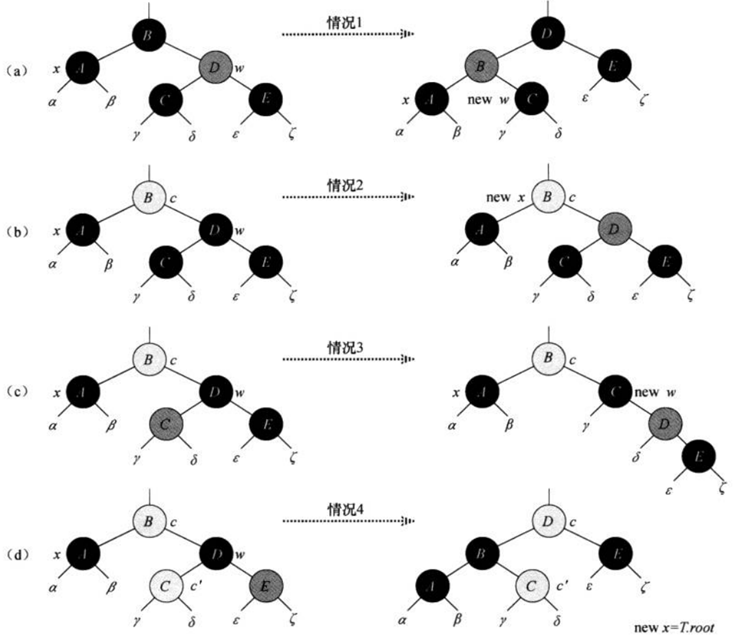
然后对每种情况给出分析(建立在x是左孩子的基础上):
Case 1:x的右兄弟w是红色,说明x的父结点一定是黑色。所作的操作是:交换w和其父结点的颜色,即把w换为黑色,其父结点换位红色;然后对父结点左旋,w重新指向x的右兄弟(该结点原本是w的左孩子,所以一定为黑色)。这是Case 1过度到Case 2或case 3或 case 4。
Case 2:w的孩子都为黑色(w也是黑色)。所作的操作是:将w换为红色,x指向其父结点。
Case 3:w的左孩子是红色,右孩子是黑色(w也是黑色)。所作的操作是:交换w和其左孩子的颜色,即把w换位红色,其左孩子换为黑色;然后对w右旋,w重新指向x的右兄弟。
Case 4:w的右孩子是黑色(w是黑色)。w与x的父结点交换颜色;并把w的右孩子设为黑色,对x的父结点左旋,x直接指向根结点,循环结束。
做完以上的while循环,我们还要做的一步操作是将根结点置为黑色。这样就能保证满足性质①。
再来看一个具体实例
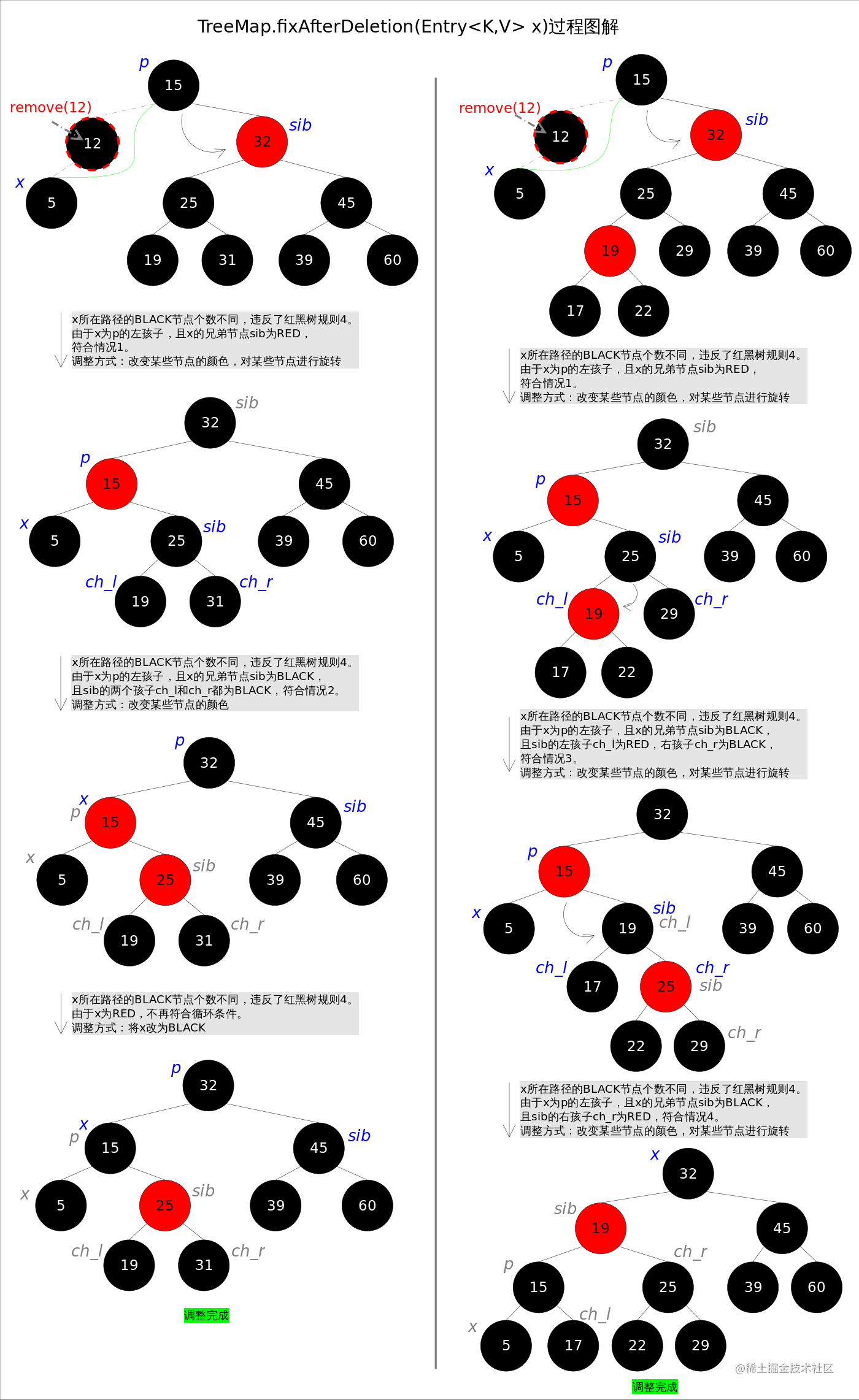
上述图解的总体思想是:将情况1首先转换成情况2,或者转换成情况3和情况4。当然,该图解并不意味着调整过程一定是从情况1开始。通过后续代码我们还会发现几个有趣的规则:a).如果是由情况1之后紧接着进入的情况2,那么情况2之后一定会退出循环(因为x为红色);b).一旦进入情况3和情况4,一定会退出循环(因为x为root)。
删除后调整函数fixAfterDeletion()的具体代码如下,其中用到了上文中提到的rotateLeft()和rotateRight()函数。通过代码我们能够看到,情况3其实是落在情况4内的。情况5~情况8跟前四种情况是对称的,因此图解中并没有画出后四种情况,读者可以参考代码自行理解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) {
if (x == x->parent->left) {
rbtree_node *w= x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_left_rotate(T, x->parent);
w = x->parent->right;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
rbtree_right_rotate(T, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rbtree_left_rotate(T, x->parent);
x = T->root;
}
} else {
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}
|
https://www.cnblogs.com/CarpenterLee/p/5525688.html#4245216