链表面试题目

反转链表

方法一：迭代
注意对于反转链表涉及到三个节点，因此需要设置3个指针，prev初始化为nullptr，curr初始化为head,而currnext指针在while迭代过程中初始化即可,另外在每一次迭代中仅需将curr节点指针反转即可

ListNode* reverseList(ListNode* head) {
    ListNode* prev=nullptr;
    ListNode* curr=head;
    ListNode* cnext;
    while(curr!=nullptr){
        cnext=cnext->next;
        curr->next=prev;
        prev=curr;
        curr=cnext;
    }
    return prev;
}

方法二：递归
这个思路是类似于后序遍历，从后往前操作节点

ListNode* reverseList(ListNode* head) {
    if (!head || !head->next) {
        return head;
    }
    ListNode* newHead = reverseList(head->next);
    head->next->next = head;
    head->next = nullptr;
    return newHead;
}

求链表倒数第K个节点

方法一：快慢指针
设置一个临时指针fast，让fast指针先走k步，之后fast与head指针一直往后走，等fast指针为nullptr时，head也走到了倒数第K个节点的位置。注意两个while循环条件都是fast指针不为nullptr

ListNode* getKthFromEnd(ListNode* head, int k) {
    ListNode *fast=head;
    while(fast!=nullptr&&k>0){
        fast=fast->next;
        k--;
    }
    while(fast!=nullptr){
        fast=fast->next;
        head=head->next;
    }
    return head;
}

方法二：求出链表长度
这个方法较为简单粗暴，先一个循环求出链表长度n，再一个循环走n-k步即可

ListNode* getKthFromEnd(ListNode* head, int k) {
    int n = 0;
    ListNode* node = nullptr;

    for (node = head; node; node = node->next) {
        n++;
    }
    for (node = head; n > k; n--) {
        node = node->next;
    }

    return node;
}

19. 删除链表的倒数第 N 个结点

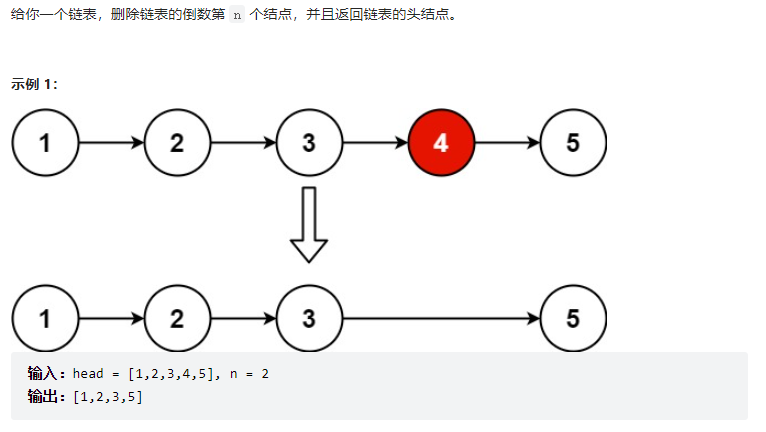
因为存在可能把头节点也给删除了，因此给当前链表新增一个头节点

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *newHead = new ListNode();
        newHead->next = head;
        ListNode *fast=newHead;
        while(fast!=nullptr&&n>0){
            fast=fast->next;
            n--;
        }

        ListNode* cur = newHead;

        while(fast->next!=nullptr){
            fast=fast->next;
            cur=cur->next;
        }
        cur->next = cur->next->next;
        return newHead->next;
    }
};

两条链表的第一个公共节点

类似于上面的先分别求出两条链表的长度，接着让长链表的指针先走abs(lenA-lenB)步，再两个链表的两个指针同时走直到相遇

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
    ListNode* tmpA=headA;ListNode* tmpB=headB;
    int lenA=0;int lenB=0;
    while(tmpA!=nullptr){
        tmpA=tmpA->next;
        lenA++;
    }     
    while(tmpB!=nullptr){
        tmpB=tmpB->next;
        lenB++;
    }

    tmpA=headA;tmpB=headB;
    if(lenA>lenB){
        while(lenA!=lenB){
            tmpA=tmpA->next;
            lenA--;
        }
    }else{
        while(lenB!=lenA){
            tmpB=tmpB->next;
            lenB--;
        }
    }

    while(tmpA!=tmpB){
        tmpA=tmpA->next;
        tmpB=tmpB->next;
    }
    return tmpA;
}

判断链表是否有环

思路就是用快慢指针，fast每次移动两格（其实三格也可以，但是两格理论上更快），slow每次移动一格，如果有环迟早会相遇

• 时间复杂度：O(N)，其中 N 是链表中的节点数。当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 N 轮。
• 空间复杂度：O(1)。我们只使用了两个指针的额外空间。

  bool hasCycle(ListNode *head) {
      if (head == nullptr || head->next == nullptr) {
              return false;
      }
      ListNode* fast=head->next;
      ListNode* slow=head;
  
      while(slow!=fast){
          if (fast == nullptr || fast->next == nullptr) {
                  return false;
          }
          fast=fast->next->next;
          slow=slow->next;
      }
  
      return true;
  }

  环的入口

遇到链表题画图是一个很好的解决办法。图来自力扣官方解答

假设快慢指针在紫色点相遇，此时慢指针走过的路程为a+b，快指针走过的路程为a+b+n(b+c)。
为什么慢指针走过a+b就必然与快指针相遇，而不是慢指针走过a+b+m(b+c)呢？

首先，由于快指针一定先进入环内，这点毋庸置疑。
而且，快指针是慢指针速度的二倍，即慢指针走完一圈，快指针可以走两圈
所以不论慢指针入环时，快指针在哪一点，快指针都可以在慢指针未走过一圈时追上慢指针。
而由于快指针走过的节点数是慢指针的二倍，所以得到公式：
(a + b) * 2 = a + b + n (b + c)
两边抵消 a+b，得到 a + b = n (b + c)
由于我们最终要求的是a，所以 a = n (b + c) - b
然而,此时慢指针在环里面所走过的路程刚好为b，如果此时有一个指针point从头开始走向环，即x路程
那么，慢指针刚好要走过的就是 n (b + c) - b + b = n (b + c)
即 point 走a的距离到达环的入口的时刻，刚好为slow走过n圈到达入口，两个指针相遇
也即point与slow两个指针相遇的时候就是那个入口！！！！

注意slow和fast都初始化为head指针

ListNode *detectCycle(ListNode *head) {
    if(head==nullptr||head->next==nullptr)return nullptr;
    ListNode* fast=head;
    ListNode* slow=head;
    while(1){
        if(fast==nullptr||fast->next==nullptr)return nullptr;
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)break;
    }
    ListNode* point=head;
    while(slow!=point){
        slow=slow->next;
        point=point->next;
    }
    return slow;
}

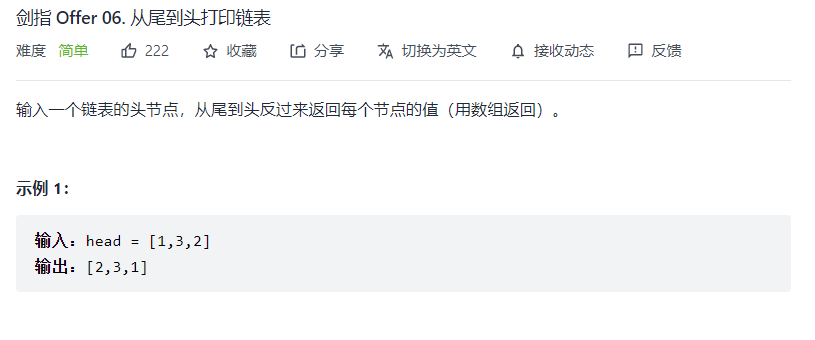
从尾到头打印链表

方法一：递归

看到逆序的就想到了递归，类似于后序遍历吧。后序遍历按后序的顺序依次对每一个节点进行操作即可。这个题目不知道为什么非得返回一个vector数组，那就按着他说的新建一个vector数组res，按照后序的顺序依次对res进行压入栈操作。

class Solution {
public:
    vector<int>res;
    vector<int> reversePrint(ListNode* head) {
        reverse(head);
        return res;
    }
    int reverse(ListNode* head){
        if(head==nullptr)return -1;
        reverse(head->next);
        res.push_back(head->val);
        return 1;
    }
};

方法二：栈

利用栈！！！

碰到逆序的竟然不想到用栈，简直是暴殄天物！！！

依次压入栈，在从栈顶移入到vector中即可。

class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        stack<int>s;
        ListNode* curr = head;
        while(curr!=nullptr){
            s.push(curr->val);
            curr = curr->next;
        }
        vector<int>ans;
        while(!s.empty()){
            ans.push_back(s.top());
            s.pop();            
        }
        return ans;
    }
};

方法三：反转链表

反转链表的操作在之前有，就不继续赘述了。主要是为什么我大脑里最先想到的是反转链表这一方法？

class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        ListNode* cnext = nullptr;
        while(curr!=nullptr){
            cnext = curr -> next;
            curr->next = prev;
            prev = curr;
            curr = cnext;
        }
        vector<int>res;
        curr = prev;
        while(curr!=nullptr){
            res.push_back(curr->val);
            curr = curr->next;
        }
        return res;
    }
};

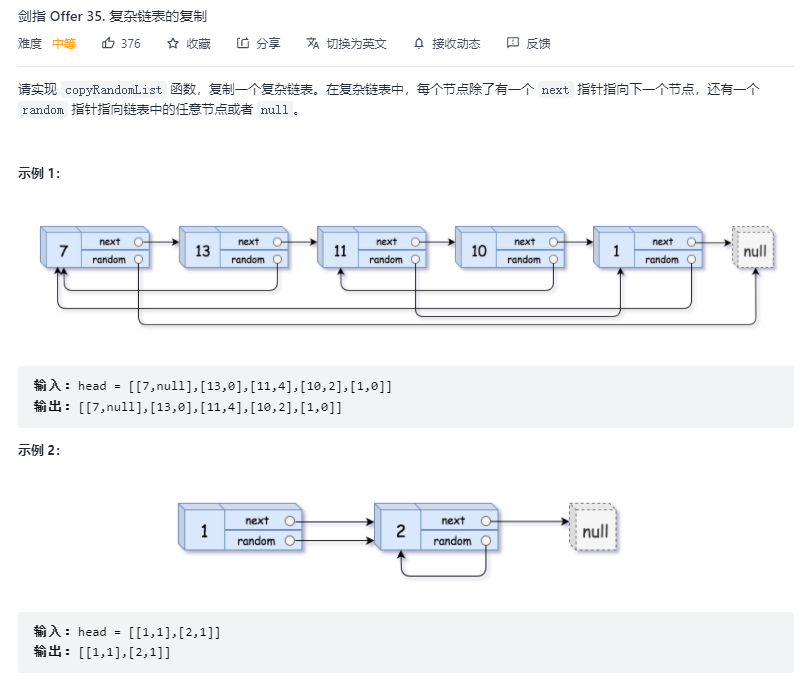
复杂链表的复制

方法一：哈希表

整体思路：
    1. 首先可能会想到双指针边遍历边复制这种方式, 但是此方式只适合普通链表的复制
        由于本题中存在 random 属性，其指向的结点是随机的，因此双指针这种方式不行（因为链表查找元素只能一个一个遍历查找）
    2. 那么问题在于，怎么使其变成可以支持快速访问呢？ --> 使用哈希表， 存储每个结点复制后的新结点；
    3. 在得到新结点与旧结点的映射关系后，怎么进行复制呢？
    4. 问题转化为 通过某种方式 将新结点按照旧结点的关系进行连线
        由于要参照旧结点的关系 ---> 一定需要遍历原始链表
    5. 连线方式：遍历到原始链表的当前结点cur, 从 map 中取出 cur 结点映射的结点 newCur, 
        我们需要做的就是 将newCur 按照 cur 在原始链表中的关系连线, 
        因为是要对 新结点 进行连线， 因此所有的结点都必须 从 map 中取对应的新结点
        newCur.next 对应的 next 在map中的映射为 map.get(cur.next);
        newCur.random 对应的 random 在 map中映射为 map.get(cur.random); 

    6. 返回头结点, 新链表的头结点也存储在 map中， 因此需要返回 map.get(head);!!!!  

class Solution {
public:
    Node* copyRandomList(Node* head) {
        unordered_map<Node*,Node*>map;
        Node* curr = head;
        while(curr!=nullptr){//先复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
            map[curr] = new Node(curr->val);
            curr = curr ->next;
        }
        curr = head;
        while(curr!=nullptr){//构建新节点的 next 和 random 指向
            map[curr]->next=map[curr->next];
            map[curr]->random=map[curr->random];
            curr = curr ->next;
        }
        return map[head];
    }
};

方法二：拼接+拆分

还没实现，先不贴代码了。

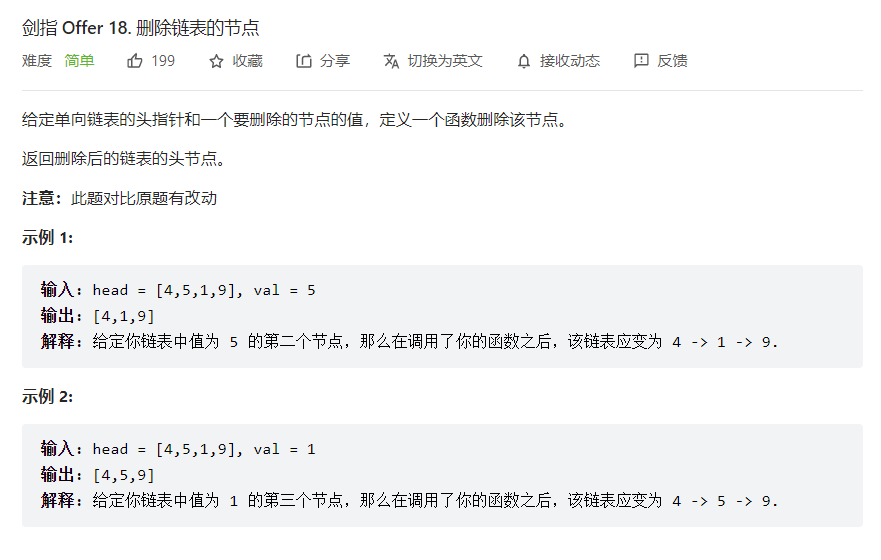
删除无表头的链表节点

方法一：迭代

较为简单

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        while(head != nullptr && head->val == val)head = head -> next;
        if(head == nullptr)return nullptr;
        ListNode* pre = head;
        ListNode* p = head -> next;
        while(p != nullptr){
            if(p->val == val){
                pre->next = p->next;
            }
            pre = p;
            p = p->next;
        }
        return head;
    }
};

方法二：递归

第一步：寻找出口，head为nullptr，直接返回即可

第二步：找出状态相同的小问题，deleteNode(head->next,val)返回以下一个节点为头节点，返回删除重复节点的头节点指针。那么分两种情况了，1.如果head->val == val，就删除head，返回deleteNode(head->next,val)即可。2.如果head->val != val，head->next = deleteNode(head->next,val)即可

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if(head == nullptr)return head;
        if(head->val == val)return deleteNode(head->next,val);
        head -> next = deleteNode(head -> next, val);
        return head;
    }
};